Logarithmic residue

of a meromorphic function at a point of the extended complex -plane

The residue

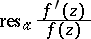of the logarithmic derivative at the point . Representing the function in a neighbourhood of a point in the form , where is a regular function in , one obtains

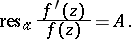The corresponding formulas for the case 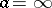have the form

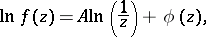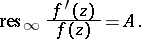If is a zero or a pole of 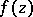of multiplicity 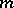, then the logarithmic residue of 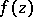at is equal to or 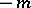, respectively; at all other points the logarithmic residue is zero.

If 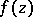is a meromorphic function in a domain and 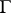is a rectifiable Jordan curve situated in 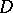and not passing through the zeros or poles of 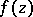, then the logarithmic residue of 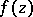with respect to the contour 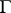is the integral

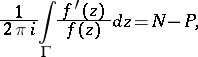(1)

where is the number of zeros and is the number of poles of inside (taking account of multiplicity). The geometrical meaning of (1) is that as is traversed in the positive sense, the vector 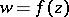performs 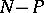rotations about the origin 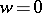of the -plane (see Argument, principle of the). In particular, if is regular in , that is, , then from (1) one obtains a formula for the calculation of the index of the point 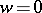with respect to the image 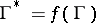of by means of the logarithmic residue:

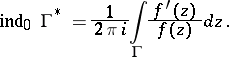(2)

Formula (2) leads to a generalization of the concept of a logarithmic residue to regular functions of several complex variables in a domain 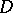of the complex space 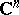, 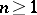. Let 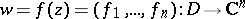be a holomorphic mapping such that the Jacobian and the set of zeros is isolated in . Then for any domain 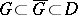bounded by a simple closed surface 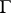not passing through the zeros of 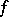one has a formula for the index of the point with respect to the image :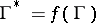

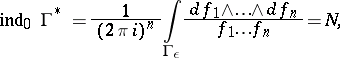(3)

where the integration is carried out with respect to the -dimensional frame 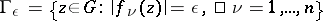with sufficiently small 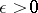. The integral in (3) also expresses the sum of the multiplicities of the zeros of in 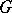(see [2]).

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian)
[2]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian)

Comments

The index of the origin with respect to a curve in the complex plane (also called the winding number of the curve, cf. Winding number) is the number of times that the curve encircles the origin. More precisely, it is the change in the argument of 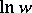as traverses the curve (cf. [a1], [a3]). In higher dimensions, the index of a point with respect to a closed surface may be defined as the number 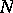such that the surface is homologous to 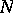times the boundary of a ball centred at the point (cf. [a2], [a4]).

References

[a1]	R.B. Burchel, "An introduction to classical complex analysis" , 1 , Acad. Press (1979)
[a2]	L.A. Aizenberg, A.P. Yuzhakov, "Integral representations and residues in multidimensional complex analysis" , Transl. Math. Monogr. , 58 , Amer. Math. Soc. (1983) (Translated from Russian)
[a3]	L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 241
[a4]	J.W. Milnor, "Toplogy from the differentiable viewpoint" , Univ. Virginia Press (1969)