Locally trivial fibre bundle

A fibre bundle (cf. Fibre space) 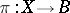with fibre 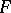such that for any point of the base 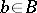there is a neighbourhood 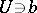and a homeomorphism 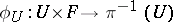such that 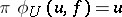, where 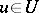, 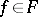. The mapping 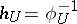is called a chart of the locally trivial bundle. The totality of charts 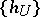associated with a covering of the base 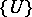forms the atlas of the locally trivial bundle. For example, a principal fibre bundle with a locally compact space and a Lie group 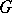is a locally trivial fibre bundle, and any chart 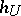satisfies the relation

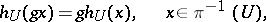where 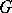acts on 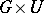according to the formula 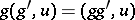. For any locally trivial fibre bundle 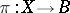and continuous mapping 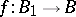the induced fibre bundle is locally trivial.

References

[1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)
[2]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)
[3]	S.-T. Hu, "Homotopy theory" , Acad. Press (1959)
[4]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)