Locally path-connected space
A topological space 
in which for any point 
and any neighbourhood 
of it there is a smaller neighbourhood 
such that for any two points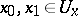 
there is a continuous mapping 
of the unit interval 
into 
with 
and 
. Any locally path-connected space is locally connected. Any open subset of a locally path-connected space is locally path-connected. A connected locally path-connected space is a path-connected space.
Locally path-connected spaces play an important role in the theory of covering spaces. Let 
be a covering and let 
be a locally path-connected space. Then a necessary and sufficient condition for a mapping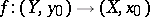 
to admit a lifting, that is, a mapping 
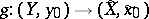such that 
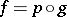, is that
 |
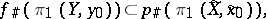where 
is the fundamental group. If 
is a locally simply-connected (locally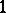 
-connected, see below) space and 
, then for any subgroup 
of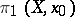 
there is a covering 
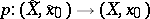for which 
.
The higher-dimensional generalization of local path-connectedness is local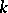 
-connectedness (local connectedness in dimension 
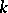). A space 
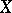is said to be locally 
-connected if for any point 
and any neighbourhood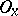 
of it there is a smaller neighbourhood 
such that any mapping of an 
-dimensional sphere 
into 
is homotopic in 
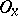to a constant mapping. A metric space 
is locally 
-connected if and only if any mapping 
from an arbitrary closed subset 
in a metric space 
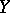with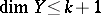 
can be extended to a neighbourhood of 
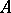in 
(the Kuratowski–Dugundji theorem).
Comments
References
| [a1] | J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1988) |
Locally path-connected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_path-connected_space&oldid=47698