Locally connected space
From Encyclopedia of Mathematics
A topological space  such that for any point
such that for any point  and any neighbourhood
and any neighbourhood  of it there is a smaller connected neighbourhood
of it there is a smaller connected neighbourhood 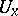 of
of  . Any open subset of a locally connected space is locally connected. Any connected component of a locally connected space is open-and-closed. A space
. Any open subset of a locally connected space is locally connected. Any connected component of a locally connected space is open-and-closed. A space 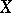 is locally connected if and only if for any family
is locally connected if and only if for any family 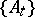 of subsets of
of subsets of 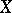 ,
,
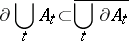 |
(here  is the boundary of
is the boundary of 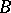 and
and 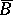 is the closure of
is the closure of 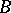 ). Any locally path-connected space is locally connected. A partial converse of this assertion is the following: Any complete metric locally connected space is locally path-connected (the Mazurkiewicz–Moore–Menger theorem).
). Any locally path-connected space is locally connected. A partial converse of this assertion is the following: Any complete metric locally connected space is locally path-connected (the Mazurkiewicz–Moore–Menger theorem).
Comments
References
| [a1] | G.L. Kelley, "General topology" , v. Nostrand (1955) pp. 61 |
| [a2] | E. Čech, "Topological spaces" , Interscience (1966) pp. §21B |
How to Cite This Entry:
Locally connected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_connected_space&oldid=47691
Locally connected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_connected_space&oldid=47691
This article was adapted from an original article by S.A. Bogatyi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article