Lipschitz integral condition
From Encyclopedia of Mathematics
A restriction on the behaviour of increase of a function in an integral metric. A function 
in a space 
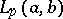with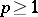 
satisfies the Lipschitz integral condition of order 
on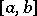 
with constant 
if
 | (*) |
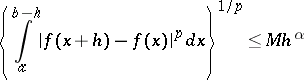for all 
. In this case one writes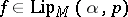 
, 
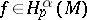or 
, 
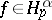. For the case of a periodic function (with period 
) the Lipschitz integral condition is defined similarly, only in inequality (*) the upper limit of integration 
must be replaced by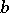 
.
References
| [1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [2] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [3] | O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , Wiley (1978) (Translated from Russian) |
How to Cite This Entry:
Lipschitz integral condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lipschitz_integral_condition&oldid=47671
Lipschitz integral condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lipschitz_integral_condition&oldid=47671
This article was adapted from an original article by A.V. Efimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article