Linear ordinary differential equation with constant coefficients
An ordinary differential equation (cf. Differential equation, ordinary) of the form
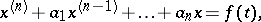 | (1) |
where 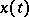 is the unknown function,
is the unknown function,  are given real numbers and
are given real numbers and 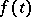 is a given real function.
is a given real function.
The homogeneous equation corresponding to (1),
 | (2) |
can be integrated as follows. Let 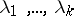 be all the distinct roots of the characteristic equation
be all the distinct roots of the characteristic equation
 | (3) |
with multiplicities  , respectively,
, respectively, 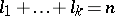 . Then the functions
. Then the functions
 | (4) |
are linearly independent (generally speaking, complex) solutions of (2), that is, they form a fundamental system of solutions. The general solution of (2) is a linear combination, with arbitrary constant coefficients, of the fundamental system of solutions. If 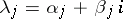 is a complex number, then for every integer
is a complex number, then for every integer 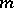 ,
,  , the real part
, the real part  and the imaginary part
and the imaginary part  of the complex solution
of the complex solution 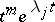 are linearly independent real solutions of (2), and to a pair of complex conjugate roots
are linearly independent real solutions of (2), and to a pair of complex conjugate roots  of multiplicity
of multiplicity  correspond
correspond 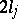 linearly independent real solutions
linearly independent real solutions
 |
The inhomogeneous equation (1) can be integrated by the method of variation of constants. If  is a quasi-polynomial, i.e.
is a quasi-polynomial, i.e.
 |
where  and
and  are polynomials of degree
are polynomials of degree  , and if the number
, and if the number  is not a root of (3), one looks for a particular solution of (1) in the form
is not a root of (3), one looks for a particular solution of (1) in the form
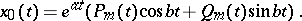 | (5) |
Here  and
and 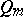 are polynomials of degree
are polynomials of degree 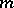 with undetermined coefficients, which are found by substituting (5) into (1). If
with undetermined coefficients, which are found by substituting (5) into (1). If  is a root of (3) of multiplicity
is a root of (3) of multiplicity 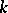 , then one looks for a particular solution of (1) in the form
, then one looks for a particular solution of (1) in the form
 |
by the method of undetermined coefficients. If  is a particular solution of the inhomogeneous equation (1) and
is a particular solution of the inhomogeneous equation (1) and  is a fundamental system of solutions of the corresponding homogeneous equation (2), then the general solution of (1) is given by the formula
is a fundamental system of solutions of the corresponding homogeneous equation (2), then the general solution of (1) is given by the formula
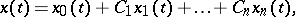 |
where  are arbitrary constants.
are arbitrary constants.
A homogeneous system of linear differential equations of order  ,
,
 | (6) |
where  is the unknown vector and
is the unknown vector and  is a constant real
is a constant real  matrix, can be integrated as follows. If
matrix, can be integrated as follows. If  is a real eigen value of multiplicity
is a real eigen value of multiplicity 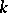 of the matrix
of the matrix  , then one looks for a solution
, then one looks for a solution 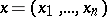 corresponding to
corresponding to 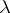 in the form
in the form
 | (7) |
Here  are polynomials of degree
are polynomials of degree  with undetermined coefficients, which are found by substituting (7) into (6); there are exactly
with undetermined coefficients, which are found by substituting (7) into (6); there are exactly 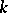 linearly independent solutions of the form (7). If
linearly independent solutions of the form (7). If 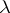 is a complex eigen value of multiplicity
is a complex eigen value of multiplicity 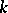 , then the real and imaginary parts of the complex solutions of the form (7) form
, then the real and imaginary parts of the complex solutions of the form (7) form  linearly independent real solutions of (6), and a pair of complex conjugate eigen values
linearly independent real solutions of (6), and a pair of complex conjugate eigen values 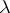 and
and  of multiplicity
of multiplicity 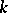 of the matrix
of the matrix  generates
generates  linearly independent real solutions of (6). Taking all eigen values of
linearly independent real solutions of (6). Taking all eigen values of  , one finds
, one finds 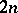 linearly independent solutions, that is, a fundamental system of solutions. The general solution of (6) is a linear combination, with arbitrary constant coefficients, of the solutions that form the fundamental system.
linearly independent solutions, that is, a fundamental system of solutions. The general solution of (6) is a linear combination, with arbitrary constant coefficients, of the solutions that form the fundamental system.
The matrix  is the fundamental matrix of the system (7), normalized at the origin, since
is the fundamental matrix of the system (7), normalized at the origin, since 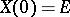 , the unit matrix. Here
, the unit matrix. Here
 |
and this matrix series converges absolutely for any matrix  and all real
and all real 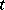 . Every other fundamental matrix of the system (6) has the form
. Every other fundamental matrix of the system (6) has the form  , where
, where 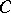 is a constant non-singular matrix of order
is a constant non-singular matrix of order  .
.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
| [2] | V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian) |
| [3] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
Linear ordinary differential equation with constant coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_ordinary_differential_equation_with_constant_coefficients&oldid=47660