Linear hypothesis
A statistical hypothesis according to which the mean  of an
of an  -dimensional normal law
-dimensional normal law  (where
(where 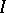 is the unit matrix), lying in a linear subspace
is the unit matrix), lying in a linear subspace  of dimension
of dimension  , belongs to a linear subspace
, belongs to a linear subspace 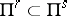 of dimension
of dimension  .
.
Many problems of mathematical statistics can be reduced to the problem of testing a linear hypothesis, which is often stated in the following so-called canonical form. Let  be a normally distributed vector with independent components and let
be a normally distributed vector with independent components and let 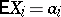 for
for  ,
, 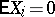 for
for  and
and  for
for 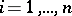 , where the quantities
, where the quantities  are unknown. Then the hypothesis
are unknown. Then the hypothesis 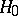 , according to which
, according to which
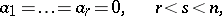 |
is the canonical linear hypothesis.
Example. Let 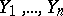 and
and 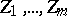 be
be  independent random variables, subject to normal distributions
independent random variables, subject to normal distributions 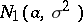 and
and 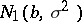 , respectively, where the parameters
, respectively, where the parameters  ,
, 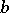 ,
, 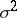 are unknown. Then the hypothesis
are unknown. Then the hypothesis 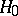 :
: 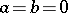 is the linear hypothesis, while a hypothesis
is the linear hypothesis, while a hypothesis  ,
,  with
with 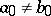 is not linear.
is not linear.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Comments
However, such a linear hypothesis 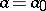 ,
,  with
with  does correspond to a linear hypothesis concerning the means of the transformed quantities
does correspond to a linear hypothesis concerning the means of the transformed quantities  ,
,  .
.
Linear hypothesis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_hypothesis&oldid=47657