Linear differential equation in a Banach space
An equation of the form
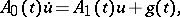 | (1) |
where 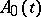 and
and 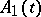 , for every
, for every 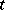 , are linear operators in a Banach space
, are linear operators in a Banach space  ,
, 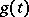 is a given function and
is a given function and  an unknown function, both with values in
an unknown function, both with values in 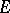 ; the derivative
; the derivative 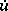 is understood to be the limit of the difference quotient with respect to the norm of
is understood to be the limit of the difference quotient with respect to the norm of 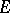 .
.
1. Linear differential equations with a bounded operator.
Suppose that 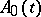 and
and 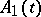 , for every
, for every 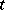 , are bounded operators acting in
, are bounded operators acting in 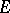 . If
. If  has a bounded inverse for every
has a bounded inverse for every  , then (1) can be solved for the derivative and takes the form
, then (1) can be solved for the derivative and takes the form
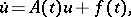 | (2) |
where 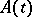 is a bounded operator in
is a bounded operator in 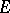 , and
, and 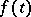 and
and 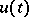 are functions with values in
are functions with values in 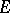 . If the functions
. If the functions 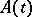 and
and 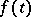 are continuous (or, more generally, are measurable and integrable on every finite interval), then the solution of the Cauchy problem
are continuous (or, more generally, are measurable and integrable on every finite interval), then the solution of the Cauchy problem
 | (3) |
exists for any 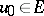 and is given by the formula
and is given by the formula
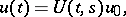 |
where
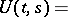 | (4) |
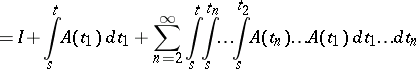 |
is the evolution operator of the equation 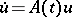 . The solution of the Cauchy problem for equation (2) is determined by the formula
. The solution of the Cauchy problem for equation (2) is determined by the formula
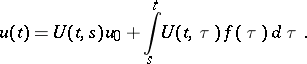 |
From (4) one obtains the estimate
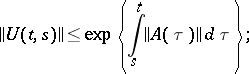 | (5) |
a refinement of it is:
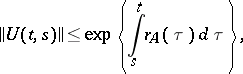 | (5prm) |
where 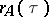 is the spectral radius of the operator
is the spectral radius of the operator 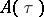 . The evolution operator has the properties
. The evolution operator has the properties
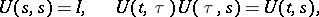 |
 |
In the study of (2) the main attention has been focused on the behaviour of its solutions at infinity, in dependence on the behaviour of 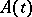 and
and 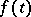 . An important characteristic of the equation is the general (or singular) exponent
. An important characteristic of the equation is the general (or singular) exponent
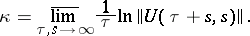 |
Equations with periodic and almost-periodic coefficients have been studied in detail (see Qualitative theory of differential equations in Banach spaces).
Equation (2) can also be considered in the complex plane. If the functions 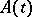 and
and 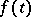 are holomorphic in a simply-connected domain containing the point
are holomorphic in a simply-connected domain containing the point  , then the formulas (3), (4), (5), (5prm) remain valid if the integrals are understood to be integrals over a rectifiable arc joining
, then the formulas (3), (4), (5), (5prm) remain valid if the integrals are understood to be integrals over a rectifiable arc joining  and
and 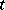 .
.
A number of other questions arises in the case when the original linear equation is not solvable for the derivative. If the operator 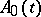 is boundedly invertible everywhere except at one point, say
is boundedly invertible everywhere except at one point, say 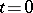 , then in the space
, then in the space 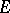 the equation reduces to the form
the equation reduces to the form
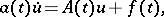 | (6) |
where 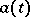 is a scalar function and
is a scalar function and 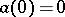 . Here the main attention is focused on the study of the behaviour of the solutions in a neighbourhood of the origin, and the analytic and non-analytic cases are distinguished.
. Here the main attention is focused on the study of the behaviour of the solutions in a neighbourhood of the origin, and the analytic and non-analytic cases are distinguished.
The analytic case.
For the simplest equation
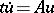 |
with a constant operator 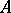 , the evolution operator
, the evolution operator 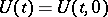 has the form
has the form
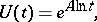 |
and the solutions are not single-valued: as one goes round the origin in the positive direction they are multiplied by the operator 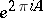 .
.
Consider an equation with a regular singularity
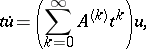 | (7) |
where the series on the right-hand side converges in a neighbourhood of the origin. If one looks for the operator 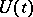 in the form of a series
in the form of a series
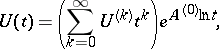 |
then for the determination of the coefficients 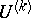 one obtains the system of equations
one obtains the system of equations
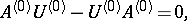 |
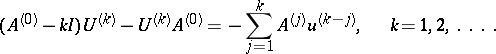 |
For this system to be solvable, that is, for (7) to be formally solvable, it is sufficient that the spectra of the operators  and
and 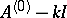 do not intersect (cf. Spectrum of an operator), or, equivalently, that there are no points differing by an integer in the spectrum of
do not intersect (cf. Spectrum of an operator), or, equivalently, that there are no points differing by an integer in the spectrum of 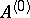 . Under this condition the series
. Under this condition the series
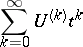 |
converges in the same neighbourhood of zero as the series for 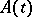 . Now, if there are finitely many integers representable as differences of points of the spectrum of
. Now, if there are finitely many integers representable as differences of points of the spectrum of 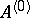 , and each of them is an isolated point of the spectrum of the transformer
, and each of them is an isolated point of the spectrum of the transformer
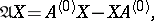 |
then there is a solution of the form
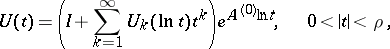 |
where the 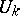 are entire functions of the argument
are entire functions of the argument 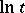 , satisfying for every
, satisfying for every  the condition
the condition
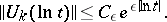 |
If the integer points of the spectrum of the transformer 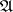 are poles of its resolvent, then the functions
are poles of its resolvent, then the functions 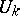 are polynomials.
are polynomials.
In the case of an irregular singularity, the differential equation
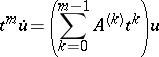 |
has been considered in a Banach algebra 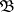 (for example, in the algebra of bounded operators on a Banach space
(for example, in the algebra of bounded operators on a Banach space 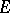 ). Under certain restrictions on
). Under certain restrictions on 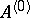 it reduces by means of Laplace integrals to an equation with a regular singularity
it reduces by means of Laplace integrals to an equation with a regular singularity 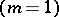 in the algebra of matrices with entries from
in the algebra of matrices with entries from 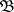 .
.
The non-analytic case.
Suppose that in the equation
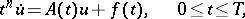 |
the functions 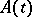 and
and 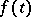 are infinitely differentiable. In the finite-dimensional case a complete result has been obtained: If the equation has a formal solution in the form of a power series, then it has a solution that is infinitely differentiable on
are infinitely differentiable. In the finite-dimensional case a complete result has been obtained: If the equation has a formal solution in the form of a power series, then it has a solution that is infinitely differentiable on 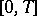 for which the formal series is the Taylor series at the point
for which the formal series is the Taylor series at the point 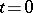 . In the infinite-dimensional case there is only a number of sufficient conditions for the existence of infinitely-differentiable solutions.
. In the infinite-dimensional case there is only a number of sufficient conditions for the existence of infinitely-differentiable solutions.
Suppose that 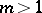 . If the spectrum of the operator
. If the spectrum of the operator 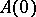 does not intersect the imaginary axis, then there is a family of infinitely-differentiable solutions that depends on an arbitrary element
does not intersect the imaginary axis, then there is a family of infinitely-differentiable solutions that depends on an arbitrary element  belonging to the invariant subspace of
belonging to the invariant subspace of 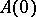 corresponding to the part of the spectrum of
corresponding to the part of the spectrum of 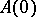 lying in the left half-plane. Any solution that is continuous on
lying in the left half-plane. Any solution that is continuous on 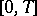 appears in this family. If the whole spectrum of
appears in this family. If the whole spectrum of 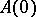 lies in the left half-plane, then there is only one infinitely-differentiable solution.
lies in the left half-plane, then there is only one infinitely-differentiable solution.
Suppose that 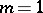 . If there are no negative integers in the spectrum of
. If there are no negative integers in the spectrum of 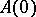 , then there is a unique infinitely-differentiable solution. Under similar assumptions about the operator
, then there is a unique infinitely-differentiable solution. Under similar assumptions about the operator 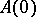 , equations of the form (6) have been considered in which
, equations of the form (6) have been considered in which 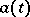 and
and 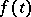 have finite smoothness, and the solutions have the same smoothness.
have finite smoothness, and the solutions have the same smoothness.
A rather different picture emerges when the differential equation is unsolvable for the derivative for all 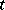 , for example when
, for example when 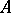 is a constant non-invertible operator. Suppose that in the equation
is a constant non-invertible operator. Suppose that in the equation
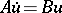 | (8) |
the operators 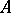 and
and 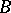 are bounded in the space
are bounded in the space 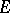 and
and 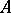 is a non-invertible Fredholm operator. Suppose that the operator
is a non-invertible Fredholm operator. Suppose that the operator 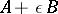 is continuously invertible for sufficiently small
is continuously invertible for sufficiently small  . Then there are decompositions into direct sums
. Then there are decompositions into direct sums 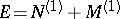 and
and 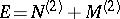 such that
such that 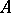 and
and 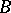 map
map 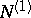 into
into 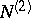 and
and 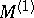 into
into 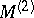 . The operator
. The operator 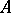 is invertible on
is invertible on 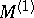 and maps onto
and maps onto 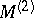 . The subspace
. The subspace 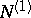 is finite-dimensional. All solutions of (8) lie in the subspace
is finite-dimensional. All solutions of (8) lie in the subspace 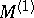 and have the form
and have the form  , where
, where 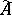 is the restriction of
is the restriction of 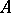 to
to 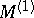 and
and 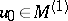 . For an inhomogeneous equation
. For an inhomogeneous equation  , a solution exists only if
, a solution exists only if 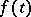 has a certain smoothness and under certain compatibility conditions for the values of
has a certain smoothness and under certain compatibility conditions for the values of 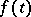 and its derivatives with the initial data. The number of derivatives that certain components of
and its derivatives with the initial data. The number of derivatives that certain components of 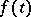 must have and the number of compatibility conditions are equal to the maximal length of
must have and the number of compatibility conditions are equal to the maximal length of 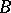 -adjoint chains of the operator
-adjoint chains of the operator 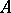 . If these conditions are satisfied, the solution of the Cauchy problem is unique.
. If these conditions are satisfied, the solution of the Cauchy problem is unique.
If the operator 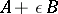 is non-invertible for all
is non-invertible for all  , then all solutions of (8) lie in a subspace that has, generally speaking, infinite deficiency (cf. also Deficiency subspace). The solution of the Cauchy problem for it is not unique. For the function
, then all solutions of (8) lie in a subspace that has, generally speaking, infinite deficiency (cf. also Deficiency subspace). The solution of the Cauchy problem for it is not unique. For the function 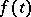 in the inhomogeneous equation infinitely many differentiability conditions and compatibility conditions are required.
in the inhomogeneous equation infinitely many differentiability conditions and compatibility conditions are required.
2. Linear differential equations with an unbounded operator.
Suppose that 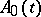 is invertible for every
is invertible for every 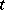 , so that (1) can be solved for the derivative and takes the form
, so that (1) can be solved for the derivative and takes the form
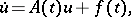 | (9) |
and suppose that here 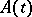 is an unbounded operator in a space
is an unbounded operator in a space 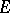 , with dense domain of definition
, with dense domain of definition 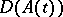 in
in 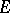 and with non-empty resolvent set, and suppose that
and with non-empty resolvent set, and suppose that 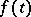 is a given function and
is a given function and 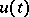 an unknown function, both with values in
an unknown function, both with values in 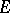 .
.
Even for the simplest equation 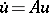 with an unbounded operator, solutions of the Cauchy problem
with an unbounded operator, solutions of the Cauchy problem 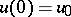 need not exist, they may be non-unique, and they may be non-extendable to the whole semi-axis, so the main investigations are devoted to the questions of existence and uniqueness of the solutions. A solution of the equation
need not exist, they may be non-unique, and they may be non-extendable to the whole semi-axis, so the main investigations are devoted to the questions of existence and uniqueness of the solutions. A solution of the equation 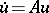 on the interval
on the interval 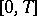 is understood to be a function that takes values in
is understood to be a function that takes values in  , is differentiable on
, is differentiable on 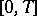 and satisfies the equation. Sometimes this definition is too rigid and one introduces the concept of a weak solution as a function that has the same properties on
and satisfies the equation. Sometimes this definition is too rigid and one introduces the concept of a weak solution as a function that has the same properties on 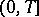 and is only continuous at
and is only continuous at  .
.
Suppose that the operator 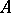 has a resolvent
has a resolvent
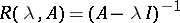 |
for all sufficiently large positive 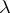 and that
and that
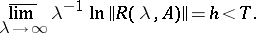 |
Then the weak solution of the problem
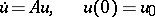 | (10) |
is unique on 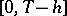 and can be branched for
and can be branched for 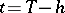 . If
. If 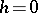 , then the solution is unique on the whole semi-axis. This assertion is precise as regards the behaviour of
, then the solution is unique on the whole semi-axis. This assertion is precise as regards the behaviour of 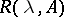 as
as 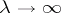 .
.
If for every 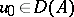 there is a unique solution of the problem (10) that is continuously differentiable on
there is a unique solution of the problem (10) that is continuously differentiable on 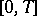 , then this solution can be extended to the whole semi-axis and can be represented in the form
, then this solution can be extended to the whole semi-axis and can be represented in the form 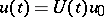 , where
, where 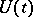 is a strongly-continuous semi-group of bounded operators on
is a strongly-continuous semi-group of bounded operators on 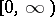 ,
, 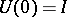 , for which the estimate
, for which the estimate 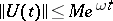 holds. For the equation to have this property it is necessary and sufficient that
holds. For the equation to have this property it is necessary and sufficient that
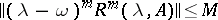 | (11) |
for all 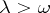 and
and 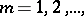 where
where 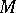 does not depend on
does not depend on 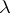 and
and 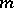 . These conditions are difficult to verify. They are satisfied if
. These conditions are difficult to verify. They are satisfied if 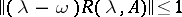 , and then
, and then  . If
. If 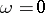 , then
, then 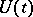 is a contraction semi-group. This is so if and only if
is a contraction semi-group. This is so if and only if 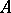 is a maximal dissipative operator. If
is a maximal dissipative operator. If 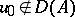 , then the function
, then the function 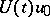 is not differentiable (in any case for
is not differentiable (in any case for 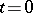 ); it is often called the generalized solution of (10). Solutions of the equation
); it is often called the generalized solution of (10). Solutions of the equation 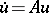 can be constructed as the limit, as
can be constructed as the limit, as 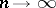 , of solutions of the equation
, of solutions of the equation 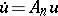 with bounded operators, under the same initial conditions. For this it is sufficient that the operators
with bounded operators, under the same initial conditions. For this it is sufficient that the operators 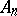 commute, converge strongly to
commute, converge strongly to 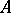 on
on 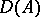 and that
and that
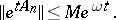 |
If the conditions (11) are satisfied, then the operators 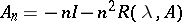 (Yosida operators) have these properties.
(Yosida operators) have these properties.
Another method for constructing solutions of the equation 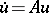 is based on Laplace transformation. If the resolvent of
is based on Laplace transformation. If the resolvent of 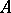 is defined on some contour
is defined on some contour 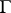 , then the function
, then the function
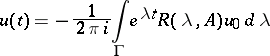 | (12) |
formally satisfies the equation
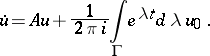 |
If the convergence of the integrals, the validity of differentiation under the integral sign and the vanishing of the last integral are ensured, then 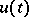 satisfies the equation. The difficulty lies in the fact that the norm of the resolvent cannot decrease faster than
satisfies the equation. The difficulty lies in the fact that the norm of the resolvent cannot decrease faster than 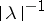 at infinity. However, on some elements it does decrease faster. For example, if
at infinity. However, on some elements it does decrease faster. For example, if 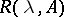 is defined for
is defined for  and if
and if
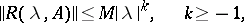 |
for sufficiently large 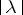 , then for
, then for 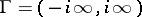 formula (12) gives a solution for any
formula (12) gives a solution for any 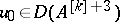 . In a "less good" case, when the previous inequality is satisfied only in the domain
. In a "less good" case, when the previous inequality is satisfied only in the domain
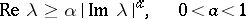 |
(weakly hyperbolic equations), and 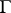 is the boundary of this domain, one obtains a solution only for an
is the boundary of this domain, one obtains a solution only for an 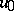 belonging to the intersection of the domains of definition of all powers of
belonging to the intersection of the domains of definition of all powers of 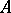 , with definite behaviour of
, with definite behaviour of 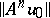 as
as 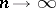 .
.
Significantly weaker solutions are obtained in the case when 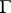 goes into the left half-plane, and one can use the decrease of the function
goes into the left half-plane, and one can use the decrease of the function 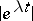 on it. As a rule, the solutions have increased smoothness for
on it. As a rule, the solutions have increased smoothness for 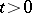 . If the resolvent is bounded on the contour
. If the resolvent is bounded on the contour 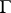 :
: 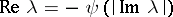 , where
, where 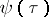 is a smooth non-decreasing concave function that increases like
is a smooth non-decreasing concave function that increases like 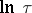 at
at 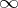 , then for any
, then for any  the function (12) is differentiable and satisfies the equation, beginning with some
the function (12) is differentiable and satisfies the equation, beginning with some 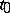 ; as
; as 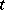 increases further, its smoothness increases. If
increases further, its smoothness increases. If 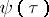 increases like a power of
increases like a power of  with exponent less than one, then the function (12) is infinitely differentiable for
with exponent less than one, then the function (12) is infinitely differentiable for 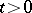 ; if
; if 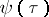 increases like
increases like 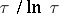 , then
, then 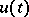 belongs to a quasi-analytic class of functions; if it increases like a linear function, then
belongs to a quasi-analytic class of functions; if it increases like a linear function, then 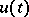 is analytic. In all these cases it satisfies the equation
is analytic. In all these cases it satisfies the equation 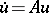 .
.
The existence of the resolvent on contours that go into the left half-plane may be obtained, by using series expansion, from the corresponding estimates on vertical lines. If for 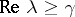 ,
,
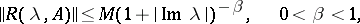 | (13) |
then for every 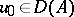 there is a solution of problem (10). All these solutions are infinitely differentiable for
there is a solution of problem (10). All these solutions are infinitely differentiable for 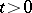 . They can be represented in the form
. They can be represented in the form 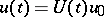 , where
, where 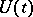 is an infinitely-differentiable semi-group for
is an infinitely-differentiable semi-group for 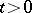 having, generally speaking, a singularity at
having, generally speaking, a singularity at  . For its derivatives one has the estimates
. For its derivatives one has the estimates
 |
If the estimate (13) is satisfied for 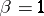 , then all generalized solutions of the equation
, then all generalized solutions of the equation 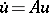 are analytic in some sector containing the positive semi-axis.
are analytic in some sector containing the positive semi-axis.
The equation 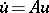 is called an abstract parabolic equation if there is a unique weak solution on
is called an abstract parabolic equation if there is a unique weak solution on 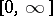 satisfying the initial condition
satisfying the initial condition 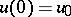 for any
for any 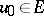 . If
. If
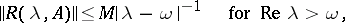 | (14) |
then the equation is an abstract parabolic equation. All its generalized solutions are analytic in some sector containing the positive semi-axis, and
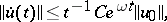 |
where 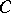 does not depend on
does not depend on 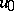 . Conversely, if the equation has the listed properties, then (14) is satisfied for the operator
. Conversely, if the equation has the listed properties, then (14) is satisfied for the operator 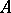 .
.
If problem (10) has a unique weak solution for any 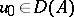 for which the derivative is integrable on every finite interval, then these solutions can be represented in the form
for which the derivative is integrable on every finite interval, then these solutions can be represented in the form 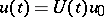 , where
, where  is a strongly-continuous semi-group on
is a strongly-continuous semi-group on 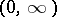 , and every weak solution of the inhomogeneous equation
, and every weak solution of the inhomogeneous equation 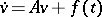 with initial condition
with initial condition 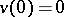 can be represented in the form
can be represented in the form
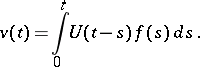 | (15) |
The function 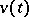 is defined for any continuous
is defined for any continuous 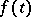 , hence it is called a generalized solution of the inhomogeneous equation. To ensure that it is differentiable, one imposes smoothness conditions on
, hence it is called a generalized solution of the inhomogeneous equation. To ensure that it is differentiable, one imposes smoothness conditions on 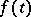 , and the "worse" the semi-group
, and the "worse" the semi-group 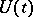 , the "higher" these should be. Thus, under the previous conditions, (15) is a weak solution of the inhomogeneous equation if
, the "higher" these should be. Thus, under the previous conditions, (15) is a weak solution of the inhomogeneous equation if 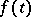 is twice continuously differentiable; if (11) is satisfied, then (15) is a solution if
is twice continuously differentiable; if (11) is satisfied, then (15) is a solution if 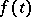 is continuously differentiable; if (13) is satisfied with
is continuously differentiable; if (13) is satisfied with 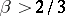 , then
, then 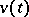 is a weak solution if
is a weak solution if 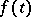 satisfies a Hölder condition with exponent
satisfies a Hölder condition with exponent 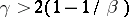 . Instead of smoothness of
. Instead of smoothness of 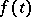 with respect to
with respect to 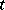 one can require that the values of
one can require that the values of 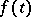 belong to the domain of definition of the corresponding power of
belong to the domain of definition of the corresponding power of 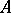 .
.
For an equation with variable operator
 | (16) |
there are some fundamental existence and uniqueness theorems about solutions (weak solutions) of the Cauchy problem 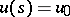 on the interval
on the interval 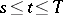 . If the domain of definition of
. If the domain of definition of 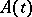 does not depend on
does not depend on 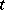 ,
,
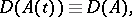 |
if the operator 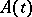 is strongly continuous with respect to
is strongly continuous with respect to 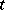 on
on 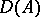 and if
and if
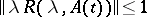 |
for 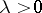 , then the solution of the Cauchy problem is unique. Moreover, if
, then the solution of the Cauchy problem is unique. Moreover, if 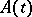 is strongly continuously differentiable on
is strongly continuously differentiable on 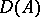 , then for every
, then for every 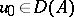 a solution exists and can be represented in the form
a solution exists and can be represented in the form
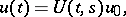 |
where 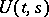 is an evolution operator with the following properties:
is an evolution operator with the following properties:
1) 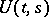 is strongly continuous in the triangle
is strongly continuous in the triangle  :
: 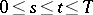 ;
;
2) 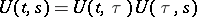 ,
, 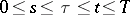 ,
, 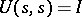 ;
;
3) 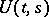 maps
maps 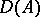 into itself and the operator
into itself and the operator
 |
is bounded and strongly continuous in 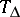 ;
;
4) on 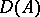 the operator
the operator 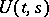 is strongly differentiable with respect to
is strongly differentiable with respect to 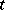 and
and  and
and
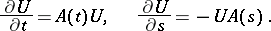 |
The construction of the operator 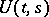 is carried out by approximating
is carried out by approximating 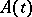 by bounded operators
by bounded operators 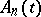 and replacing the latter by piecewise-constant operators.
and replacing the latter by piecewise-constant operators.
In many important problems the previous conditions on the operator 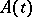 are not satisfied. Suppose that for the operator
are not satisfied. Suppose that for the operator 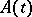 there are constants
there are constants 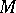 and
and 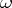 such that
such that
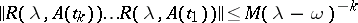 |
for all 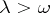 ,
, 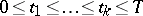 ,
,  . Suppose that in
. Suppose that in 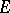 there is densely imbedded a Banach space
there is densely imbedded a Banach space 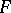 contained in all the
contained in all the 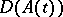 and having the following properties: a) the operator
and having the following properties: a) the operator 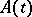 acts boundedly from
acts boundedly from 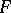 to
to 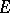 and is continuous with respect to
and is continuous with respect to 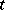 in the norm as a bounded operator from
in the norm as a bounded operator from 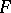 to
to 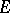 ; and b) there is an isomorphism
; and b) there is an isomorphism 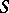 of
of 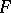 onto
onto 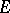 such that
such that
 |
where 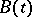 is an operator function that is bounded in
is an operator function that is bounded in 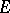 and strongly measurable, and for which
and strongly measurable, and for which 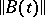 is integrable on
is integrable on 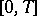 . Then there is an evolution operator
. Then there is an evolution operator 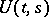 having the properties: 1); 2); 3')
having the properties: 1); 2); 3') 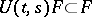 and
and 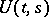 is strongly continuous in
is strongly continuous in 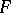 on
on 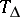 ; and 4') on
; and 4') on 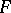 the operator
the operator 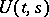 is strongly differentiable in the sense of the norm of
is strongly differentiable in the sense of the norm of 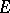 and
and 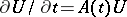 ,
, 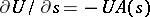 . This assertion makes it possible to obtain existence theorems for the fundamental quasi-linear equations of mathematical physics of hyperbolic type.
. This assertion makes it possible to obtain existence theorems for the fundamental quasi-linear equations of mathematical physics of hyperbolic type.
The method of frozen coefficients is used in the theory of parabolic equations. Suppose that, for every 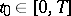 , to the equation
, to the equation 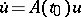 corresponds an operator semi-group
corresponds an operator semi-group  . The unknown evolution operator formally satisfies the integral equations
. The unknown evolution operator formally satisfies the integral equations
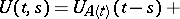 |
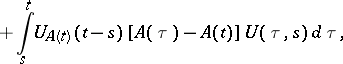 |
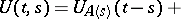 |
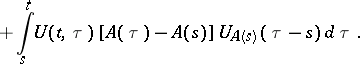 |
When the kernels of these equations have weak singularities, one can prove that the equation has solutions and also that 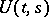 is an evolution operator. The following statement has the most applications: If
is an evolution operator. The following statement has the most applications: If
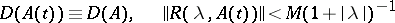 |
for 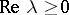 and
and
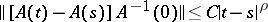 |
(a Hölder condition), then there is an evolution operator 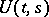 that gives a weak solution
that gives a weak solution 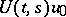 of the Cauchy problem for every
of the Cauchy problem for every 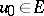 . Uniqueness of the solution holds under the single condition that the operator
. Uniqueness of the solution holds under the single condition that the operator 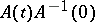 is continuous (in a Hilbert space). An existence theorem similar to the one given above holds for the operator
is continuous (in a Hilbert space). An existence theorem similar to the one given above holds for the operator 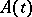 with a condition of type (13) and for a certain relation between
with a condition of type (13) and for a certain relation between 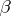 and
and 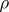 .
.
The assumption that 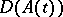 is constant does not make it possible in applications to consider boundary value problems with boundary conditions depending on
is constant does not make it possible in applications to consider boundary value problems with boundary conditions depending on 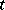 . Suppose that
. Suppose that
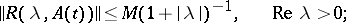 |
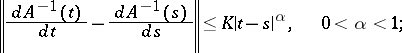 |
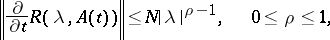 |
in the sector 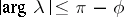 ,
, 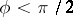 ; then there is an evolution operator
; then there is an evolution operator 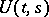 . Here it is not assumed that
. Here it is not assumed that 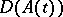 is constant. There is a version of the last statement adapted to the consideration of parabolic problems in non-cylindrical domains, in which
is constant. There is a version of the last statement adapted to the consideration of parabolic problems in non-cylindrical domains, in which 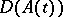 for every
for every 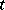 lies in some subspace
lies in some subspace  of
of 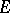 .
.
The operator 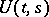 for equation (16) formally satisfies the integral equation
for equation (16) formally satisfies the integral equation
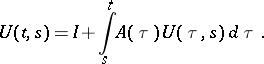 | (17) |
Since 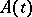 is unbounded, this equation cannot be solved by the method of successive approximation (cf. Sequential approximation, method of). Suppose that there is a family of Banach spaces
is unbounded, this equation cannot be solved by the method of successive approximation (cf. Sequential approximation, method of). Suppose that there is a family of Banach spaces 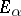 ,
, 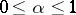 , having the property that
, having the property that 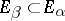 and
and 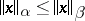 for
for 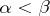 . Suppose that
. Suppose that 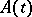 is bounded as an operator from
is bounded as an operator from 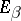 to
to 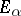 :
:
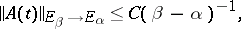 |
and that 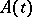 is continuous with respect to
is continuous with respect to 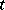 in the norm of the space of bounded operators from
in the norm of the space of bounded operators from 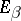 to
to 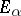 . Then in this space the method of successive approximation for equation (17) will converge for
. Then in this space the method of successive approximation for equation (17) will converge for 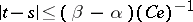 . In this way one can locally construct an operator
. In this way one can locally construct an operator 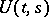 as a bounded operator from
as a bounded operator from 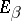 to
to 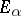 . In applications this approach gives theorems of Cauchy–Kovalevskaya type (cf. Cauchy–Kovalevskaya theorem).
. In applications this approach gives theorems of Cauchy–Kovalevskaya type (cf. Cauchy–Kovalevskaya theorem).
For the inhomogeneous equation (9) with known evolution operator, for the equation 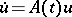 the solution of the Cauchy problem is formally written in the form
the solution of the Cauchy problem is formally written in the form
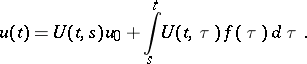 |
This formula can be justified in various cases under certain smoothness conditions on  .
.
References
| [1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 MR0617913 Zbl 0435.46002 |
| [2] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) MR0342804 Zbl 0179.20701 |
| [3] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) MR0089373 Zbl 0392.46001 Zbl 0033.06501 |
| [4] | , Functional analysis , Math. Reference Library , Moscow (1972) (In Russian) |
| [5] | V.P. Glushko, "Degenerate linear differential equations" , Voronezh (1972) (In Russian) Zbl 0265.34011 Zbl 0252.34072 Zbl 0241.34008 Zbl 0235.34011 |
| [6] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) MR0352638 |
| [7] | S.P. Zubova, K.I. Chernyshovas, "A linear differential equation with a Fredholm operator acting on the derivative" , Differential Equations and their Applications , 14 , Vilnius (1976) pp. 21–29 (In Russian) (English abstract) MR0470716 |
| [8] | A.N. Kuznetsov, "Differentiable solutions to degenerate systems of ordinary equations" Funct. Anal. Appl. , 6 : 2 (1972) pp. 119–127 Funktional. Anal. i Prilozhen. , 6 : 2 (1972) pp. 41–51 Zbl 0259.34005 |
| [9] | S.G. Krein, G.I. Laptev, "An abstract scheme for the consideration of parabolic problems in noncylindrical regions" Differential Eq. , 5 (1969) pp. 1073–1081 Differentsial. Uravn. , 5 : 8 (1969) pp. 1458–1469 Zbl 0254.35064 |
| [10] | Yu.I. Lyubich, "The classical and local Laplace transformation in an abstract Cauchy problem" Russian Math. Surveys , 21 : 3 (1966) pp. 1–52 Uspekhi Mat. Nauk , 21 : 3 (1966) pp. 3–51 Zbl 0173.12002 |
| [11] | L.V. Ovsyannikov, "A singular operator in a scale of Banach spaces" Soviet Math. Dokl. , 6 (1965) pp. 1025–1028 Dokl. Akad. Nauk SSSR , 163 : 4 (1965) pp. 819–822 Zbl 0144.39003 |
| [12] | P.E. Sobolevskii, "Equations of parabolic type in a Banach space" Trudy Moskov. Mat. Obshch. , 10 (1961) pp. 297–350 (In Russian) MR0141900 |
| [13] | R. Beals, "Laplace transform methods for evolution equations" H.G. Garnir (ed.) , Boundary value problems for linear evolution equations: partial differential equations. Proc. NATO Adv. Study Inst. Liège, 1976 , Reidel (1977) pp. 1–26 MR0492648 Zbl 0374.35039 |
| [14] | A. Friedman, "Uniqueness of solutions of ordinary differential inequalities in Hilbert space" Arch. Rat. Mech. Anal. , 17 : 5 (1964) pp. 353–357 MR0171181 Zbl 0143.16701 |
| [15] | T. Kato, "Linear evolution equations of "hyperbolic" type II" J. Math. Assoc. Japan , 25 : 4 (1973) pp. 648–666 MR0326483 Zbl 0262.34048 |
| [16] | F. Trèves, "Basic linear partial differential equations" , Acad. Press (1975) MR0447753 Zbl 0305.35001 |
| [17] | J. Miller, "Solution in Banach algebras of differential equations with irregular singular point" Acta Math. , 110 : 3–4 (1963) pp. 209–231 MR0153939 Zbl 0122.35303 |
Linear differential equation in a Banach space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_differential_equation_in_a_Banach_space&oldid=47651