Lindeberg-Feller theorem

A theorem that establishes necessary and sufficient conditions for the asymptotic normality of the distribution function of sums of independent random variables that have finite variances. Let 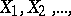be a sequence of independent random variables with means 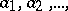and finite variances 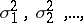not all of which are zero. Let

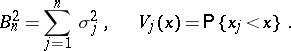In order that

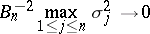and

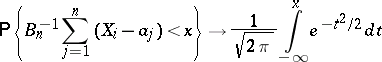for any as , it is necessary and sufficient that the following condition (the Lindeberg condition) is satisfied:

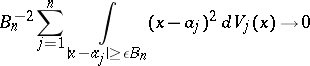as 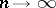for any 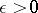. Sufficiency was proved by J.W. Lindeberg [1] and necessity by W. Feller [2].

References

[1]	J.W. Lindeberg, "Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung" Math. Z. , 15 (1922) pp. 211–225
[2]	W. Feller, "Ueber den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung" Math. Z. , 40 (1935) pp. 521–559
[3]	M. Loève, "Probability theory" , Springer (1977)
[4]	V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian)