Limit-absorption principle

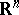A manner for uniquely finding solutions to equations analogous to the Helmholtz equation by introducing an infinitesimal absorption. Mathematically the principle is as follows. Let be an unbounded region in , let 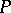be the self-adjoint operator on 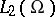given by the differential expression 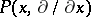, , 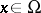and homogeneous boundary conditions on and let 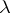be a point in the continuous spectrum of 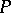. Then for 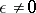the equation

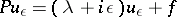is uniquely solvable in 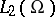, and in certain cases it is possible to find solutions 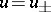of the equation

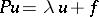by the limit transition

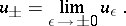It is assumed here that 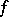has compact support and the convergence 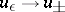, as 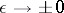, is understood in the sense of 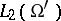, where 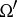is an arbitrary bounded set in . Since 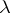is a point of the continuous spectrum of 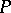, the limit in 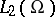does not exist, in general.

The first limit-absorption principle was formulated for the Helmholtz equation in 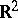(cf. [1]):

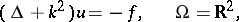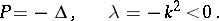The solutions 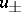found using this principle are diverging or converging waves and satisfy the radiation conditions at infinity. These results were carried over (cf. [2], [3]) to elliptic boundary value problems in the exterior of bounded regions in 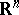for an operator

(*)

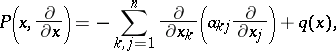where the coefficients 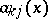tend to constants sufficiently rapidly as 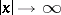. In order that the limit-absorption principle holds in this case it is necessary that 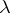is not an eigen value of 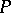or that 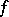is orthogonal to the eigen functions. A theorem of T. Kato (cf. [3]) gives sufficient conditions for the absence of eigen values in the continuous spectrum of the operator 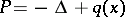. Such a theorem has been obtained for the operator (*) (cf. [3]). The limit-absorption principle has been substantiated for certain regions with non-compact boundary (cf. [3], [4]).

A limit-absorption principle and corresponding radiation conditions have been found for higher-order equations and for systems of equations (cf. [5]–[7]); they consist of the following. Let 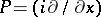be an elliptic (or hypo-elliptic) operator satisfying: 1) the polynomial 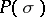has real coefficients; 2) the surface 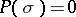, , 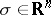decomposes into connected smooth surfaces 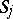, , 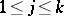whose curvatures do not vanish; and 3) 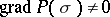on 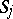. Suppose that an orientation is given on 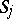, i.e. for each surface one has independently chosen a normal direction . 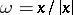Let , let 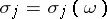be a point on 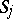at which and 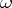have identical direction and let 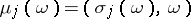. Then the function 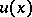does satisfy the radiation conditions if it can be represented as

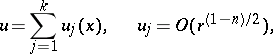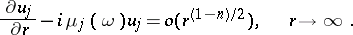These conditions determine a unique solution of the equation

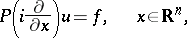for any function 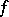with compact support. The limit-absorption principle for this equation is that this solution can be obtained as the limit, for 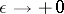, of the unique solution 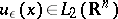of the elliptic equation

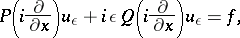where 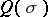has real coefficients and 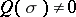on 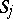. Depending on the choice of 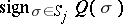, , 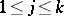one obtains in the limit solutions satisfying the radiation conditions corresponding to some orientation of 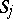. This principle has been substantiated for higher-order equations and systems with variable coefficients in the exterior of bounded regions (cf. [5]–[7]), as well as in the case of non-convex 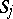. For such equations there is also a uniqueness theorem of Kato type.

References

[1]	W. [V.S. Ignatovskii] Ignatowsky, "Reflexion elektromagnetischer Wellen an einem Drahte" Ann. der Physik , 18 : 13 (1905) pp. 495–522
[2]	A.Ya. Povzner, "On the decomposition of arbitrary functions into eigenfunctions of the operator 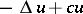" Mat. Sb. , 32 : 1 (1953) pp. 109–156 (In Russian)
[3]	D.M. Eidus, "The principle of limiting amplitude" Russian Math. Surveys , 24 : 3 (1969) pp. 97–167 Uspekhi Mat. Nauk , 24 : 3 (1969) pp. 91–156
[4]	A.V. Sveshnikov, "The limit absorption principle for a wave guide" Dokl. Akad. Nauk SSSR , 80 : 3 (1951) pp. 345–347 (In Russian)
[5]	B.R. Vainberg, "Principles of radiation, limit absorption and limit amplitude in the general theory of partial differential equations" Russian Math. Surveys , 21 : 3 (1966) pp. 115–193 Uspekhi Mat. Nauk , 21 : 3 (1966) pp. 115–194
[6]	B.R. Vainberg, "On elliptic problems in unbounded domains" Math. USSR Sb. , 4 (1968) pp. 419–444 Mat. Sb. , 75 : 3 (1968) pp. 454–480
[7]	B.R. Vainberg, "Asymptotic methods in equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian)