Levi condition
A condition, which can be effectively verified, for pseudo-convexity in the sense of Levi of domains in the complex space 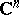 . It was proposed by E.E. Levi
. It was proposed by E.E. Levi
and consists of the following. Suppose that a domain 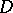 is specified in a neighbourhood
is specified in a neighbourhood 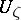 of a boundary point
of a boundary point 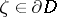 by the condition
by the condition
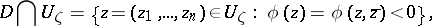 |
where the real function 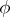 belongs to the class
belongs to the class  and
and 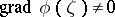 . If
. If  is Levi pseudo-convex at
is Levi pseudo-convex at 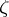 , then the (complex) Hessian
, then the (complex) Hessian
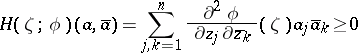 | (1) |
is non-negative for all 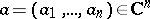 that are complex orthogonal to
that are complex orthogonal to 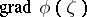 , that is, are such that
, that is, are such that
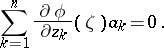 | (2) |
Conversely, if the condition
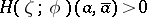 | (3) |
is satisfied at the point  for all
for all 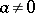 satisfying (2), then
satisfying (2), then 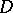 is Levi pseudo-convex at
is Levi pseudo-convex at 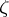 .
.
For 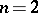 the inequalities (1) and (3) given above can be replaced by the simpler equivalent inequalities
the inequalities (1) and (3) given above can be replaced by the simpler equivalent inequalities  and
and 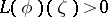 , respectively, where
, respectively, where
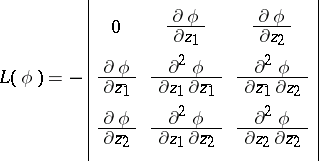 |
is the determinant of the Levi function 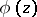 .
.
The Levi condition (1)–(3) has also been generalized to domains on complex manifolds (see [4]).
References
| [1a] | E.E. Levi, "Studii sui punti singolari essenziali delle funzioni analiticke de due o più variabili complesse" Ann. Mat. Pura Appl. , 17 (1910) pp. 61–87 |
| [1b] | E.E. Levi, "Sulle ipersurficie dello spazio a 4 dimensione che possono essere frontiera del campo di esistenza di una funzione analitica di due variabili complesse" Ann. Mat. Pura Appl. , 18 (1911) pp. 69–79 |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
Comments
By definition, 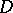 is Levi pseudo-convex at
is Levi pseudo-convex at 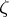 if (1) is satisfied for vectors that satisfy (2);
if (1) is satisfied for vectors that satisfy (2);  is called strictly (Levi) pseudo-convex at
is called strictly (Levi) pseudo-convex at 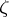 if (3) is satisfied for vectors that satisfy (2).
if (3) is satisfied for vectors that satisfy (2).
The domain 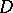 is called (Levi) pseudo-convex if it is Levi pseudo-convex at every boundary point.
is called (Levi) pseudo-convex if it is Levi pseudo-convex at every boundary point.
For domains with 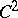 boundary, Levi pseudo-convexity is equivalent with any of the following:
boundary, Levi pseudo-convexity is equivalent with any of the following:
a) 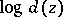 is plurisubharmonic on
is plurisubharmonic on  (i.e.
(i.e.  is Hartogs pseudo-convex), where
is Hartogs pseudo-convex), where 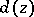 denotes the Euclidean distance of
denotes the Euclidean distance of  to the boundary of
to the boundary of 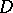 .
.
b) 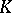 relatively compact in
relatively compact in 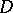 implies
implies 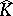 relatively compact in
relatively compact in 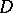 , where
, where 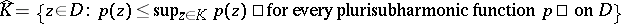 .
.
References
| [a1] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
Levi condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Levi_condition&oldid=47619