Level lines
of a Green function
The point sets
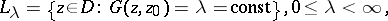 |
where  is the Green function for the domain
is the Green function for the domain 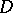 in the complex plane with pole at the point
in the complex plane with pole at the point  . If
. If 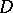 is simply connected, then the structure of this set is easily determined by conformally mapping
is simply connected, then the structure of this set is easily determined by conformally mapping 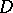 onto the disc
onto the disc 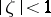 , taking the point
, taking the point 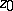 to
to  . The Green function is invariant under this transformation, while the level lines of the Green function for the disc
. The Green function is invariant under this transformation, while the level lines of the Green function for the disc 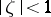 with pole at
with pole at 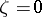 , i.e.
, i.e. 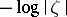 , are the circles
, are the circles 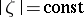 . So, in the case of a simply-connected domain, the level line
. So, in the case of a simply-connected domain, the level line 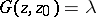 is a simple closed curve, coinciding for
is a simple closed curve, coinciding for  with the boundary of
with the boundary of 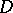 and tending to
and tending to 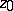 as
as  . If the domain
. If the domain 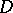 is
is 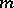 -connected and its boundary consists of Jordan curves
-connected and its boundary consists of Jordan curves  ,
, 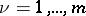 , then: if
, then: if  is sufficiently large, the level line is a Jordan curve; for
is sufficiently large, the level line is a Jordan curve; for  the corresponding level line tends to the point
the corresponding level line tends to the point 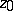 , while for decreasing
, while for decreasing 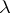 it moves away from
it moves away from 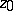 ; if
; if  , then for certain values of
, then for certain values of 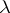 the level line has self-intersection, and decomposes into non-intersecting simple closed curves; for sufficiently small
the level line has self-intersection, and decomposes into non-intersecting simple closed curves; for sufficiently small 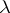 the level line consists of
the level line consists of 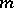 Jordan curves and for
Jordan curves and for  each of these curves tends to one of the boundary curves of
each of these curves tends to one of the boundary curves of 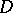 .
.
In questions of the approximation of functions by polynomials on a closed bounded set  with a simply-connected complement, an important role is played by estimates for the distance between boundary points of
with a simply-connected complement, an important role is played by estimates for the distance between boundary points of 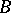 and level lines of the complement of
and level lines of the complement of 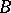 (cf. [4], [5]).
(cf. [4], [5]).
For univalent conformal mappings of the disc 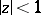 by functions of the class
by functions of the class 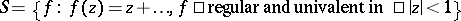 (cf. Univalent function), the behaviour of the level line
(cf. Univalent function), the behaviour of the level line 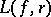 (the image of the circle
(the image of the circle 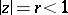 ) intuitively gives the degree of distortion. Any function of class
) intuitively gives the degree of distortion. Any function of class 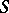 maps the disc
maps the disc 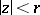 ,
,  , onto a convex domain, while the disc
, onto a convex domain, while the disc  ,
, 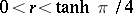 , is mapped onto a star-like domain. The level line
, is mapped onto a star-like domain. The level line 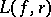 ,
,  ,
,  , belongs to the annulus
, belongs to the annulus
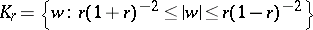 |
and bounds a simply-connected domain comprising the coordinate origin.
For the curvature 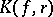 of the level line
of the level line 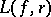 in the class
in the class 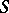 one has the following sharp estimate:
one has the following sharp estimate:
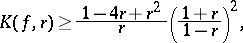 |
and equality holds only for the function 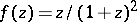 at the point
at the point  . The exact upper bound for
. The exact upper bound for 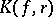 in the class
in the class 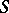 is at present (1984) not known. The exact upper bound for
is at present (1984) not known. The exact upper bound for 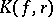 in the subclass of star-like functions in
in the subclass of star-like functions in 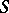 (cf. Star-like function) has the form
(cf. Star-like function) has the form
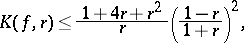 |
and equality holds only for the function  at
at  .
.
For mappings of the disc 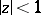 by functions of the class
by functions of the class 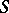 the number of points of inflection of the level line
the number of points of inflection of the level line 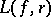 and the number of points violating the star-likeness condition (i.e. points of the level line at which the direction of rotation of the radius vector changes when
and the number of points violating the star-likeness condition (i.e. points of the level line at which the direction of rotation of the radius vector changes when  runs over the circle
runs over the circle  in a given direction) may change non-monotonically for increasing
in a given direction) may change non-monotonically for increasing  , i.e. if
, i.e. if 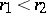 , one can show that the level line
, one can show that the level line 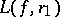 may have more points of inflection and more points violating the star-likeness condition than
may have more points of inflection and more points violating the star-likeness condition than 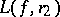 .
.
References
| [1] | S. Stoilov, "The theory of functions of a complex variable" , 1 , Moscow (1962) (In Russian; translated from Rumanian) |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) pp. Appendix (Translated from Russian) |
| [3] | I.A. Aleksandrov, "Parametric extensions in the theory of univalent functions" , Moscow (1976) (In Russian) |
| [4] | V.K. Dzyadyk, "On a problem of S.M. Nikol'skii in a complex region" Izv. Akad. Nauk SSSR Mat. , 23 : 5 (1959) pp. 697–763 (In Russian) |
| [5] | N.A. Lebedev, N.A. Shirokov, "The uniform approximation of functions on closed sets with a finite number of angular points with non-zero exterior angles" Izv. Akad. Nauk Armen. SSR Ser. Mat. , 6 : 4 (1971) pp. 311–341 (In Russian) |
Comments
Some non-Soviet references for the approximation questions mentioned are [a1] and [a2], in which other references can be found. See also Approximation of functions of a complex variable.
References
| [a1] | L. Bijvoets, W. Hogeveen, J. Korevaar, "Inverse approximation theorems of Lebedev and Tamrazov" P.L. Butzer (ed.) , Functional analysis and approximation (Oberwolfach 1980) , Birkhäuser (1981) pp. 265–281 |
| [a2] | D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980) pp. Chapt. 1, §6 |
Level lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Level_lines&oldid=47617