Lah number
From Encyclopedia of Mathematics
A coefficient in the expansion
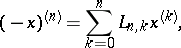 |
where
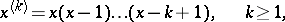 |
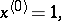 |
are the falling factorials.
Replacing  by
by 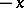 , it follows that
, it follows that
 |
The Lah numbers are given explicitly by
 |
 |
and they are tabulated in [a1] for  .
.
The numbers satisfy the recurrence relation
 |
and have the generating function
 |
They are related to Stirling numbers of the first and second kinds (cf. Combinatorial analysis), and to Bell polynomials (cf. Bell polynomial) by
 |
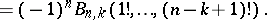 |
See also [a4] for a connection with Laguerre polynomials.
If 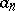 and
and 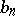 are sequences, then
are sequences, then
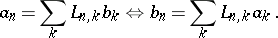 |
References
| [a1] | L. Comtet, "Advanced combinatorics" , Reidel (1974) |
| [a2] | I. Lah, "Eine neue Art von Zahlen, ihre Eigenschaften und Anwendung in der mathematischen Statistik" Mitteil. Math. Statist. , 7 (1955) pp. 203–216 |
| [a3] | J. Riordan, "Combinatorial analysis" , Wiley (1958) |
| [a4] | S. Roman, "The umbral calculus" , Acad. Press (1984) |
How to Cite This Entry:
Lah number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lah_number&oldid=47568
Lah number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lah_number&oldid=47568
This article was adapted from an original article by E.K. Lloyd (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article