Lagrangian manifold

An -dimensional differentiable submanifold 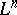of a 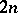-dimensional symplectic manifold 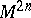such that the exterior form 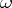specifying the symplectic structure on 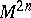vanishes identically on 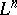(that is, for any point 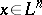and any vectors 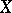and 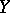which are tangent to 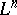at this point one has 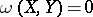). In the most important case, when 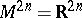with coordinates (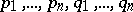) and 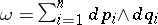, the condition that the submanifold 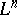given by the parametric equations

is Lagrangian, has the form

where 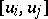is the Lagrange bracket.

References

[1]	V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian)
[2]	V.P. Maslov, "Introduction to the method of phase integrals (the WKB method)" , Moscow (1965) (In Russian) (Appendix to the Russian translation of: J. Heading, The WKB method in the multi-dimensional case)
[3]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)
[4]	V.P. Maslov, M.V. Fedoryuk, "Quasi-classical approximation for the equations of quantum mechanics" , Reidel (1981) (Translated from Russian)
[5]	A.S. Mishchenko, B.Yu. Sternin, V.E. Shatalov, "Lagrangian manifolds and the method of the canonical operator" , Moscow (1978) (In Russian)
[6]	V.I. [V.I. Arnol'd] Arnold, A.B. [A.B. Givent'al] Giventhal, "Symplectic geometry" , Dynamical Systems , IV , Springer (1988) (Translated from Russian)

Comments

Also often called Lagrangian submanifold.

References

[a1]	P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French)
[a2]	I. Vaismann, "Symplectic geometry and secondary characteristic classes" , Birkhäuser (1987)