Lagrange stability

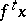A property of a point (a trajectory ) of a dynamical system (or 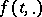, cf. [2]) given on a metric space 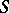, requiring that the trajectory is contained in a pre-compact set (cf. Pre-compact space).

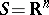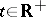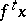If , then Lagrange stability is the same as boundedness of the trajectory. If for all (respectively, for all ) the point is contained in a pre-compact set, then the trajectory 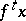(the point ) is called positively (respectively, negatively) Lagrange stable. The concept of Lagrange stability was introduced by H. Poincaré in connection with analyzing the results of J.L. Lagrange on the stability of planetary orbits.

Birkhoff's theorem: If 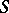is complete, then the closure of a positively or negatively Lagrange-stable trajectory contains at least one compact minimal set. Every point of a compact minimal set is a recurrent point.

References

[1]	H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , 3 , Blanchard, reprint (1987) pp. Chapt. 26
[2]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)

Comments

In [1], Poincaré explicitly introduces the term "stabilité à la Poisson" , but merely implicitly suggests the notion "stabilité à la Lagrange" by mentioning that boundedness of the planetary orbits was proved by Lagrange.

The above definitions can be given for any dynamical system, not necessarily defined on a metric space. In particular, for the first part of Birkhoff's theorem as formulated above, it is not necessary to require that 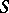is metrizable, let alone complete. Metrizability and completeness are needed to prove that every point of a minimal set is a recurrent point. In the general case, every point of a compact minimal set is an almost-periodic point.