Lagrange interpolation formula

A formula for obtaining a polynomial of degree (the Lagrange interpolation polynomial) that interpolates a given function at nodes :

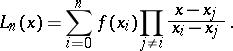(1)

When the are equidistant, that is, , using the notation one can reduce (1) to the form

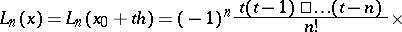(2)

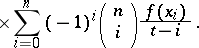In the expression (2), called the Lagrange interpolation formula for equidistant nodes, the coefficients

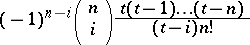of the 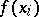are called the Lagrange coefficients.

If 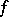has a derivative of order 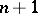on the interval 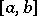, if all interpolation nodes lie in this interval and if for any point 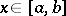one defines

then a point 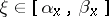exists such that

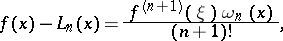where

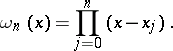If the absolute value of the derivative 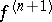is bounded on 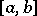by a constant 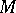and if the interpolation nodes are chosen such that the roots of the Chebyshev polynomial of degree 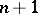are mapped into these points under a linear mapping from onto , then for any 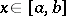one has

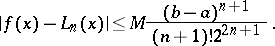If the interpolation nodes are complex numbers and lie in some domain bounded by a piecewise-smooth contour 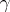, and if 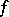is a single-valued analytic function defined on the closure of 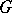, then the Lagrange interpolation formula has the form

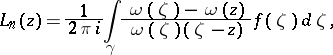where

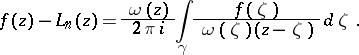The Lagrange interpolation formula for interpolation by means of trigonometric polynomials is:

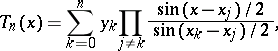which is a trigonometric polynomial of order having prescribed values at the given nodes .

The formula was proposed by J.L. Lagrange in 1795.

References

[1]	I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)
[2]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)

References

[a1]	P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126
[a2]	L.W. Johnson, R.D. Riess, "Numerical analysis" , Addison-Wesley (1977)
[a3]	G.M. Phillips, P.J. Taylor, "Theory and applications of numerical analysis" , Acad. Press (1973)