Lacunary system
of order 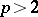 ,
, 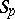 -system
-system
An orthonormal system of functions 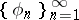 of the space
of the space 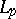 such that if the series
such that if the series
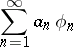 | (*) |
converges in 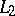 , then its sum belongs to
, then its sum belongs to 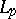 . If the system of functions
. If the system of functions 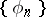 is an
is an 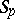 -system for any
-system for any 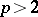 , it is called an
, it is called an 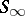 -system. S. Banach proved (see [2]) that from any sequence of functions bounded in
-system. S. Banach proved (see [2]) that from any sequence of functions bounded in 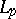 and orthonormal in
and orthonormal in 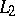 one can extract an
one can extract an 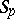 -system. For an orthonormal system of functions
-system. For an orthonormal system of functions 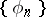 to be an
to be an 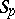 -system it is necessary and sufficient that there is a constant
-system it is necessary and sufficient that there is a constant 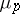 depending only on
depending only on 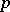 and such that
and such that
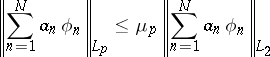 |
for all  and
and 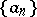 . If
. If 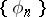 is an
is an 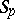 -system for some
-system for some 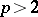 , then there is a constant
, then there is a constant  such that
such that
 |
for all  and
and 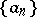 . A system of functions with this property is called a Banach system. These definitions extend to non-orthogonal systems of functions (see [3], for example). Sometimes a lacunary system of functions is understood to be a system of functions whose series have one or several properties of lacunary trigonometric series, in dependence on which they take different names. For example, with the theory of uniqueness for lacunary trigonometric series there is associated the concept of a lacunary system of
. A system of functions with this property is called a Banach system. These definitions extend to non-orthogonal systems of functions (see [3], for example). Sometimes a lacunary system of functions is understood to be a system of functions whose series have one or several properties of lacunary trigonometric series, in dependence on which they take different names. For example, with the theory of uniqueness for lacunary trigonometric series there is associated the concept of a lacunary system of  -uniqueness. A system
-uniqueness. A system 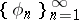 is called a system of
is called a system of  -uniqueness if there is a number
-uniqueness if there is a number 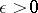 such that the convergence of the series (*) to zero everywhere, except possibly on a set of measure less than
such that the convergence of the series (*) to zero everywhere, except possibly on a set of measure less than  , implies that all its coefficients are zero.
, implies that all its coefficients are zero.
References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
| [2] | G. Alexits, "Konvergenzprobleme der Orthogonalreihen" , Deutsch. Verlag Wissenschaft. (1960) |
| [3] | V.F. Gaposhkin, "Lacunary series and independent functions" Russian Math. Surveys , 21 : 6 (1966) pp. 1–82 Uspekhi Mat. Nauk , 21 : 6 (1966) pp. 3–82 |
Lacunary system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lacunary_system&oldid=47551