Kähler metric

Kählerian metric

A Hermitian metric on a complex manifold whose fundamental form 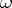is closed, i.e. satisfies the condition 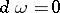. Examples: the Hermitian metric in ; the Fubini–Study metric on the complex projective space ; and the Bergman metric (see Bergman kernel function) in a bounded domain in . A Kähler metric on a complex manifold induces a Kähler metric on any submanifold. Any Hermitian metric on a one-dimensional manifold is a Kähler metric.

The concept was first studied by E. Kähler [1]. At the same time, in algebraic geometry systematic use was made of a metric on projective algebraic varieties induced by the Fubini–Study metric (see [5]). This is a Hodge metric, i.e. its fundamental form has integral periods.

A Hermitian metric 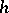on a complex manifold is a Kähler metric if and only if it satisfies any one of the following conditions: parallel transfer along any curve (relative to the Levi-Civita connection) is a complex linear mapping, i.e. it commutes with the complex structure operator; the complex Laplacian corresponding to the metric on differential forms satisfies the condition 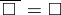, i.e. the Laplace operator 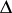is precisely 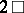; local coordinates can be introduced in a neighbourhood of any point, relative to which the matrix of 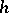coincides with the identity matrix up to second-order quantities (see [3], [6]).

References

[1]	E. Kähler, "Ueber eine bemerkenswerte Hermitesche Metrik" Abh. Math. Sem. Univ. Hamburg , 9 (1933) pp. 173–186
[2]	A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958)
[3]	A. Lichnerowicz, "Global theory of connections and holonomy groups" , Noordhoff (1976) (Translated from French)
[4]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)
[5]	W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952)
[6]	P. Deligne, P. Griffiths, J. Morgan, D. Sullivan, "The real homology of Kaehler manifolds" Invent. Math. , 29 (1975) pp. 245–274

Comments

On a complex manifold a Hermitian metric 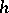can be expressed in local coordinates by a Hermitian symmetric tensor:

where is a positive-definite Hermitian (symmetric) matrix (i.e. and 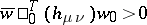for all 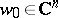). The associated fundamental form is then