Kuratowski set

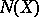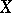A one-dimensional set in the plane, which is -dimensional at all its points with the exception of a countable set. First constructed by C. Kuratowski [1] in connection with the problem of the dimension of the subset of a given -dimensional space consisting of all points 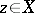at which

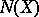( is called the dimensional kernel of 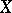.) For a metric space 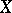with a countable base it is always the case that

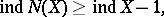and the Kuratowski set shows that this result is best possible.

The Kuratowski set is constructed as follows. Let 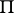be the Cantor set in the closed interval 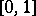of the horizontal axis in a Cartesian coordinate system on the plane. For each

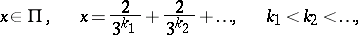put

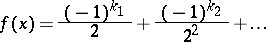and . The graph of this function, i.e. the set 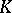of points 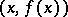, , 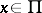on the plane, is the Kuratowski set. If is 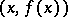, where is the right-hand end point of an interval adjacent to 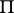, then 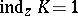, but 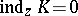at all other points.

References

[1]	C. Kuratowski, "Une application des images de fonctions à la construction de certains ensembles singuliers" Mathematica , 6 (1932) pp. 120–123
[2]	P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian)

Comments

The Kuratowski set is not a continuum, since it is neither compact (for compact metric spaces the equality 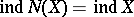holds) nor connected (it is even totally disconnected, since it admits a continuous one-to-one mapping onto : ).

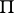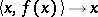The Kuratowski set is, however, completely metrizable.

A separable metric space 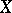such that 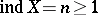and such that the dimensional kernel of 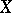has dimension 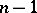, is sometimes called weakly -dimensional.

The Kuratowski set is weakly 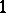-dimensional.

The first example of such a space was given by W. Sierpiński [a2]. For weakly -dimensional spaces for 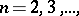cf. [a3], [a4].

References

[a1]	R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50
[a2]	W. Sierpiński, "Sur les ensembles connexes et non-connexes" Fund. Math. , 2 (1921) pp. 81–95
[a3]	S. Mazurkiewicz, "Sur les ensembles de dimension faibles" Fund. Math. , 13 (1929) pp. 210–217
[a4]	B. Tomaszewski, "On weakly -dimensional spaces" Fund. Math. , 103 (1979) pp. 1–8