Kronecker formula
A formula for the algebraic sum of the values of a function on the set of roots of a system of equations; established by L. Kronecker , [2]. Let 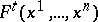 ,
, 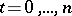 , and
, and 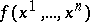 be real-valued continuously differentiable functions on
be real-valued continuously differentiable functions on 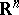 such that the system of equations
such that the system of equations
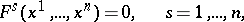 | (1) |
has a finite number of roots. Suppose that the equation
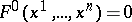 |
defines a closed surface 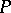 not passing through the roots of the system (1), and that
not passing through the roots of the system (1), and that 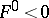 in the interior of
in the interior of 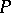 . If the functions
. If the functions 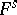 ,
, 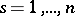 , are considered as components of a vector field on
, are considered as components of a vector field on 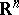 , then their singular points (by definition) coincide with the roots of the system (1). Let
, then their singular points (by definition) coincide with the roots of the system (1). Let 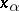 be some root and let
be some root and let 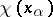 be its index as a singular point (cf. Singular point, index of a). Then
be its index as a singular point (cf. Singular point, index of a). Then
 | (2) |
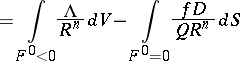 |
(summation over all roots), where 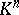 is the surface area of the unit sphere
is the surface area of the unit sphere 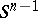 ,
,
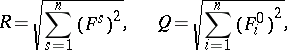 |
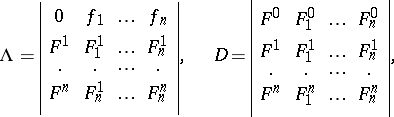 |
and, if 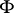 is any function,
is any function, 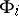 denotes the derivative
denotes the derivative 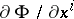 . Formula (2) is Kronecker's formula.
. Formula (2) is Kronecker's formula.
If 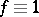 , the space integral in (2) disappears, and one obtains an expression for the sum of the indices
, the space integral in (2) disappears, and one obtains an expression for the sum of the indices 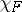 of the singular points of the vector field
of the singular points of the vector field 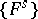 in the interior of the surface
in the interior of the surface 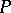 , i.e. an expression for the degree of the mapping from the surface
, i.e. an expression for the degree of the mapping from the surface  into the sphere
into the sphere 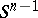 obtained by restricting the mapping
obtained by restricting the mapping 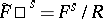 ,
, 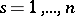 , to
, to 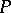 . Under certain additional assumptions,
. Under certain additional assumptions, 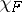 is equal to the so-called Kronecker characteristic of the system of functions
is equal to the so-called Kronecker characteristic of the system of functions 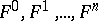 (see [3]).
(see [3]).
References
| [1a] | L. Kronecker, "Ueber Systeme von Funktionen mehrer Variablen. Erster Abhandlung" Monatsberichte (1869) pp. 159–193 |
| [1b] | L. Kronecker, "Ueber Systeme von Funktionen mehrer Variablen. Zweite Abhandlung" Monatsberichte (1869) pp. 688–698 |
| [2] | L. Kronecker, "Ueber Sturm'sche Funktionen" Monatsberichte (1878) pp. 95–121 |
| [3] | N.G. Chetaev, "Stability of motion. Studies in analytical mechanics" , Moscow (1946) (In Russian) |
| [4a] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 7 (1881) pp. 375–422 |
| [4b] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 8 (1882) pp. 251–296 |
| [4c] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 1 (1885) pp. 167–244 |
| [4d] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 2 (1886) pp. 151–217 |
Comments
Kronecker's characteristic of a system of functions is the origin of the notion of the Degree of a mapping. Cf. [a1] for historical remarks.
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 5, Sect. 3 |
Kronecker formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker_formula&oldid=47527