Kontorovich-Lebedev-transform(2)
From Encyclopedia of Mathematics
The integral transform
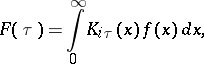 |
where 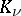 is the Macdonald function.
is the Macdonald function.
If 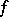 is of bounded variation in a neighbourhood of a point
is of bounded variation in a neighbourhood of a point  and if
and if
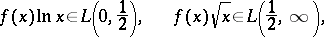 |
then the following inversion formula holds:
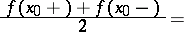 |
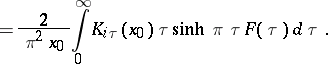 |
Let 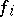 ,
, 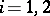 , be real-valued functions with
, be real-valued functions with
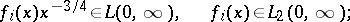 |
and let
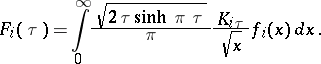 |
Then
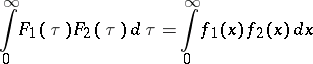 |
(Parseval's identity).
The finite Kontorovich–Lebedev transform has the form
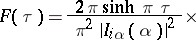 |
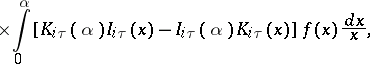 |
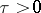 , where
, where 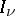 is the modified Bessel function (see [3]).
is the modified Bessel function (see [3]).
The study of such transforms was initiated by M.I. Kontorovich and N.N. Lebedev (see [1], [2]).
References
| [1] | M.I. Kontorovich, N.N. Lebedev, "A method for the solution of problems in diffraction theory and related topics" Zh. Eksper. i. Toer. Fiz. , 8 : 10–11 (1938) pp. 1192–1206 (In Russian) |
| [2] | N.N. Lebedev, Dokl. Akad. Nauk SSSR , 52 : 5 (1945) pp. 395–398 |
| [3] | Ya.S. Uflyand, E. Yushkova, Dokl. Akad. Nauk SSSR , 164 : 1 (1965) pp. 70–72 |
| [4] | V.A. Ditkin, A.P. Prudnikov, "Integral transforms and operational calculus" , Pergamon (1965) (Translated from Russian) |
Comments
A transform table for the Kontorovich–Lebedev transform can be found in [a1]. A treatment in some detail of the transform is in [a2].
References
| [a1] | A. Erdelyi, W. Magnus, F. Oberhettinger, "Tables of integral transforms" , 1–2 , McGraw-Hill (1954) pp. Chapt. XII |
| [a2] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) pp. Chapt. 6 |
How to Cite This Entry:
Kontorovich-Lebedev-transform(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kontorovich-Lebedev-transform(2)&oldid=47518
Kontorovich-Lebedev-transform(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kontorovich-Lebedev-transform(2)&oldid=47518
This article was adapted from an original article by Yu.A. BrychkovA.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article