Kirchhoff method

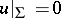A method for approximately solving problems in the theory of the diffraction of short waves; proposed by G.R. Kirchhoff. In its simplest version Kirchhoff's method amounts to the following: Let a wave process be described by the Helmholtz equation and consider the problem of the scattering of a plane wave by a convex surface on which the classical (Dirichlet) boundary condition holds. The solution reduces to finding a function satisfying the Helmholtz equation subject to the indicated boundary condition and representable as the sum , where satisfies the Sommerfeld radiation conditions. The solution of the problem exists and it has the integral representation

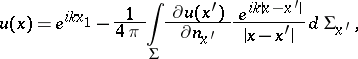(1)

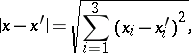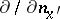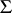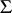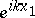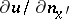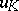where is the derivative along the normal to . The normal is taken outward relative to the infinite domain bounded internally by . It is assumed that on the part of illuminated by the plane wave , is approximately equal to the expression obtained by the ray method. On the shadowed part one sets . The expression obtained in this way is called the Kirchhoff approximation for .

In the illuminated region, and the geometric approximation for are the same in their principal terms. In a neighbourhood of the boundary between the illuminated and shadowed zones, the principal term of the asymptotic expansion of 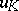is expressed in terms of the Fresnel integral 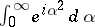, and in the shadowed zone (in fact in the shadowed zone decreases considerably faster than ).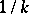

The Kirchhoff method gives a formula for that is correct in the principal terms and remains correct as . In the subsequent orders in 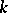the Kirchhoff approximation is no longer applicable.

References

[1]	H. Hönl, A.-W. Maue, K. Westpfahl, "Theorie der Beugung" S. Flügge (ed.) , Handbuch der Physik , 25/1 , Springer (1961) pp. 218–573

References

[a1]	A. Rubinowicz, "Die Beugungswelle in der Kirchhoffschen Theorie der Beugung" , PWN (1957)