Khinchin inequality
From Encyclopedia of Mathematics
for independent functions
An estimate in 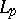 of the sum of independent functions (cf. Independent functions, system of). Suppose that
of the sum of independent functions (cf. Independent functions, system of). Suppose that 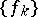 is a system of independent functions and that for some
is a system of independent functions and that for some 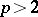 ,
,
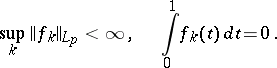 |
Then
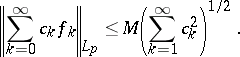 |
If
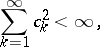 |
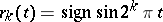 is a Rademacher function (cf. Rademacher system) and if
is a Rademacher function (cf. Rademacher system) and if
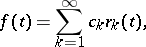 |
then for any 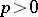 ,
,
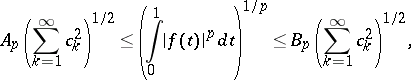 |
where 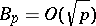 as
as 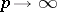 . This inequality was established by A.Ya. Khinchin in [1]. The exact value of
. This inequality was established by A.Ya. Khinchin in [1]. The exact value of 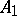 is
is 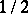 .
.
An analogue of the Khinchin inequality is valid in Banach spaces [4]. There exists a constant 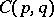 ,
, 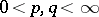 , such that for any element
, such that for any element 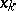 in a Banach space
in a Banach space 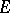 ,
,
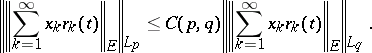 |
One of the numerous applications of the Khinchin inequality is as follows: If
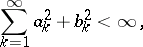 |
then for almost-all choices 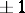 the function
the function
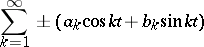 |
belongs to all 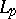 ,
, 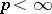 (see [5]).
(see [5]).
References
| [1] | A.Ya. Khinchin, "Ueber dyadische Brüche" Math. Z. , 18 (1923) pp. 109–116 |
| [2] | S. Karlin, "Orthogonal properties of independent functions" Trans. Amer. Math. Soc. , 66 (1949) pp. 44–64 |
| [3] | V.F. Gaposhkin, "Lacunary series and independent functions" Russian Math. Surveys , 21 : 6 (1966) pp. 1–82 Uspekhi Mat. Nauk , 21 (1966) pp. 3–82 |
| [4] | J.-P. Kahane, "Some random series of functions" , Cambridge Univ. Press (1985) |
| [5] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Khinchin inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Khinchin_inequality&oldid=47497
Khinchin inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Khinchin_inequality&oldid=47497
This article was adapted from an original article by E.M. Semenov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article