Kerr metric

The solution of the Einstein equation describing the external gravity field of a rotating source with mass and angular momentum . It is of type according to the classification of A.Z. Petrov. The simplest description is as the Kerr–Schild metric:

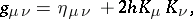where is the null vector , tangent to the special principal null congruence with rotation (of non-gradient type), and is the metric tensor of Minkowski space. The characteristic parameter of the Kerr metric is . In the general case in the presence of a charge (a Kerr–Newman metric) the scalar function has the form

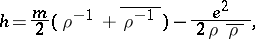where

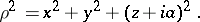The field is singular on the annular thread of radius (when ). For the singularity contracts to a point; when the Kerr metric becomes the Schwarzschild metric.

The Kerr metric was obtained by R.P. Kerr [1].

References

[1]	R.P. Kerr, "Gravitational field of a spinning mass as an example of algebraically special matrices" Phys. Rev. Letters , 11 (1963) pp. 237–238
[2]	C.W. Misner, K.S. Thorne, J.A. Wheeler, "Gravitation" , Freeman (1973)
[3]	M. Rees, R. Ruffini, J. Wheeler, "Black holes, gravitational waves and cosmology" , Gordon & Breach (1974)