Kernel of a complex sequence

The set of points in the extended complex plane that for a sequence is defined as follows. Let be the smallest closed convex domain in the complex plane that contains 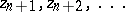. If there is no half-plane containing these points, then is the whole complex plane, including the point at infinity; if such half-planes exist, then is their common part. The point at infinity belongs to if is unbounded, and does not if is bounded. The intersection is called the kernel of the sequence .

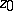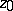If is bounded, then its kernel coincides with the closed convex hull of the set of limit points; if converges to , , then the kernel is . The kernel of a real sequence is the interval of the real line with end points:

The kernel of a sequence cannot be empty, although it may consist only of the point at infinity, as, for example, for where . A sequence with kernel consisting of the point at infinity is sometimes called definitely divergent. For a real sequence this means that or .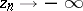

Questions of kernel inclusion of summation methods are considered in the theory of summability. A summation method is kernel-stronger than a summation method on a set 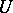of sequences if for any , where and are, respectively, the kernels of and , that is, of sequences of averages of .

References

[1a]	K. Knopp, "Zur Theorie des Limitierungsverfahren I" Math. Z. , 31 (1930) pp. 97–127
[1b]	K. Knopp, "Zur Theorie des Limitierungsverfahren II" Math. Z. , 31 (1930) pp. 276–305
[2]	R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950)
[3]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)