Jordan lemma

Let be a regular analytic function of a complex variable , where , , 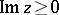up to a discrete set of singular points. If there is a sequence of semi-circles

such that the maximum 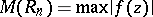on 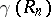tends to zero as 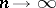, then

where is any positive number. Jordan's lemma can be applied to residues not only under the condition 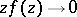, but even when uniformly on a sequence of semi-circles in the upper or lower half-plane. For example, in order to calculate integrals of the form

Obtained by C. Jordan [1].

References

[1]	C. Jordan, "Cours d'analyse" , 2 , Gauthier-Villars (1894) pp. 285–286
[2]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1967) (In Russian)
[3]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6

References

[a1]	D.S. Mitrinović, J.D. Kečkić, "The Cauchy method of residues: theory and applications" , Reidel (1984)