Join

of two topological spaces and

The topological space, denoted by , and defined as the quotient space of the product by the decomposition whose elements are the sets (), (), and the individual points of the set .

Examples. If 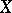consists of a single point, then is the cone over . is homeomorphic to the 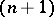-fold suspension over 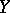. In particular, 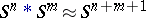. The operation of join is commutative and associative (at least in the category of locally compact Hausdorff spaces). For calculating the homology of a join (with coefficients in a principal ideal domain), an analogue of the Künneth formula is used:

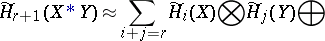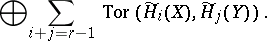The join of an -connected space and an -connected space is -connected. The operation of join lies at the basis of Milnor's construction of a universal principal fibre bundle.

Comments

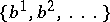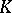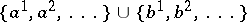Let and be (abstract) simplicial complexes with vertices and , respectively. Then the join of and is the simplicial complex with vertices whose simplices are all subsets of the form 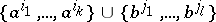for which 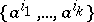is a simplex of 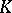and 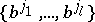is a simplex o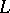f . If 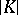denotes a geometric realization of a simplicial complex 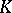, then is (homeomorphic to) .

References

[a1]	S. Lefschetz, "Topology" , Chelsea, reprint (1965) pp. Sect. 47 (Chapt. II §8)
[a2]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 25; 437–444
[a3]	C.R.F. Maunder, "Algebraic topology" , v. Nostrand-Reinhold (1970)