Jensen inequality
in the simplest discrete form
The inequality
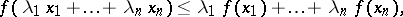 | (1) |
where 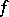 is a convex function on some set
is a convex function on some set 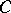 in
in 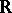 (see Convex function (of a real variable)),
(see Convex function (of a real variable)), 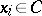 ,
, 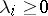 ,
, 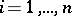 , and
, and
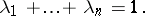 |
Equality holds if and only if 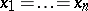 or if
or if 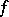 is linear. Jensen's integral inequality for a convex function
is linear. Jensen's integral inequality for a convex function 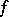 is:
is:
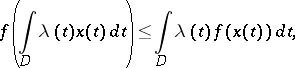 | (2) |
where 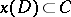 ,
,  for
for 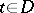 and
and
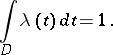 |
Equality holds if and only if either 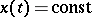 on
on 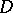 or if
or if 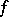 is linear on
is linear on 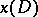 . If
. If 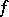 is a concave function, the inequality signs in (1) and (2) must be reversed. Inequality (1) was established by O. Hölder, and (2) by J.L. Jensen [2].
is a concave function, the inequality signs in (1) and (2) must be reversed. Inequality (1) was established by O. Hölder, and (2) by J.L. Jensen [2].
With suitable choices of the convex function 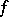 and the weights
and the weights 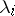 or weight function
or weight function 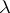 , inequalities (1) and (2) become concrete inequalities, among which one finds the majority of the classical inequalities. For example, if in (1) one sets
, inequalities (1) and (2) become concrete inequalities, among which one finds the majority of the classical inequalities. For example, if in (1) one sets 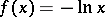 ,
, 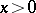 , then one obtains an inequality between the weighted arithmetic mean and the geometric mean:
, then one obtains an inequality between the weighted arithmetic mean and the geometric mean:
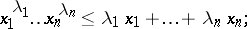 | (3) |
for 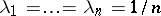 , inequality (3) takes the form
, inequality (3) takes the form
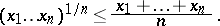 |
References
| [1] | O. Hölder, "Ueber einen Mittelwertsatz" Göttinger Nachr. (1889) pp. 38–47 |
| [2] | J.L. Jensen, "Sur les fonctions convexes et les inégualités entre les valeurs moyennes" Acta Math. , 30 (1906) pp. 175–193 |
| [3] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
Comments
Jensen's inequality (2) can be generalized by taking instead a probability measure  on a
on a 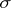 -algebra
-algebra 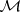 in a set
in a set 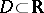 ,
,  a bounded real-valued function in
a bounded real-valued function in 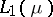 and
and 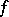 a convex function on the range of
a convex function on the range of  ; then
; then
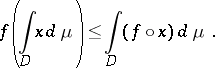 |
For another generalization cf. [a2].
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1978) pp. 24 |
| [a2] | P.S. Bullen, D.S. Mitrinović, P.M. Vasić, "Means and their inequalities" , Reidel (1988) pp. 27ff |
Jensen inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jensen_inequality&oldid=47465