Jacobi brackets
From Encyclopedia of Mathematics
Mayer brackets
The differential expression
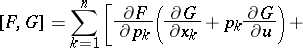 | (1) |
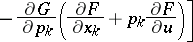 |
in the functions 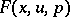 and
and  of
of 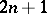 independent variables
independent variables 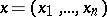 and
and 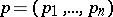 .
.
The main properties are:
1) 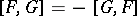 ;
;
2) 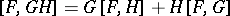 ;
;
3) if 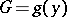 ,
, 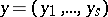 and
and 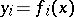 , then
, then 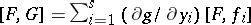 ;
;
4) 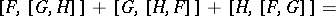
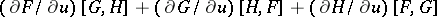 .
.
The last property is called the Jacobi identity (see [1], [2]).
The expression (1) is sometimes written in the form
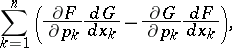 |
where the symbolic notation
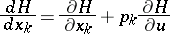 | (2) |
is used. If  and
and 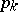 are regarded as functions of
are regarded as functions of 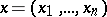 , and
, and 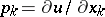 ,
, 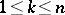 , then (2) gets the meaning of the total derivative with respect to
, then (2) gets the meaning of the total derivative with respect to 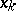 .
.
If 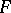 and
and 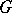 are independent of
are independent of  , then their Jacobi brackets (1) are Poisson brackets.
, then their Jacobi brackets (1) are Poisson brackets.
References
| [1] | C.G.J. Jacobi, "Nova methodus, aequationes differentiales partiales primi ordinis inter numerum variabilium quemcunque propositas integrandi" J. Reine Angew. Math. , 60 (1862) pp. 1–181 |
| [2] | A. Mayer, "Ueber die Weiler'sche Integrationsmethode der partiellen Differentialgleichungen erster Ordnung" Math. Ann. , 9 (1876) pp. 347–370 |
| [3] | N.M. Gyunter, "Integrating first-order partial differential equations" , Leningrad-Moscow (1934) (In Russian) |
| [4] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
The Poisson brackets are an essential tool in classical mechanics, cf. e.g. [a1].
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
How to Cite This Entry:
Jacobi brackets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_brackets&oldid=47454
Jacobi brackets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_brackets&oldid=47454
This article was adapted from an original article by A.P. Soldatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article