Jackson singular integral

Jackson operator

An integral of the form

in which the expression

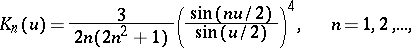is known as a Jackson kernel. It was first employed by D. Jackson [1] in his estimate of the best approximation of a function 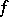in the modulus of continuity 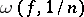or in the modulus of continuity of its derivative of order . Jackson's singular integral is a positive operator and is a trigonometric polynomial of order 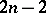; its kernel 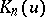can be represented in the form

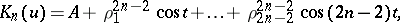where 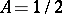and 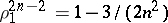, 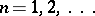. The estimate

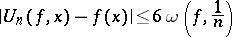is valid.

References

[1]	D. Jackson, "The theory of approximation" , Amer. Math. Soc. (1930)
[2]	I.P. Natanson, "Constructive function theory" , 1–3 , F. Ungar (1964–1965) (Translated from Russian)