Isocline
of a first-order differential equation
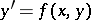 |
A set of points in the 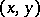 -plane at which the inclinations of the direction field defined by equation
-plane at which the inclinations of the direction field defined by equation
are one and the same. If 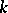 is an arbitrary real number, then the
is an arbitrary real number, then the 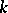 -isocline of equation
-isocline of equation
is the set
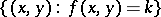 |
(in general, this is a curve); at each of its points the (oriented) angle between the  -axis and the tangent to the solution of
-axis and the tangent to the solution of
going through the point is  . For example, the
. For example, the  -isocline is defined by the equation
-isocline is defined by the equation  and consists of just those points of the
and consists of just those points of the 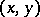 -plane at which the solutions of equation
-plane at which the solutions of equation
have horizontal tangents. The 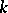 -isocline of
-isocline of
is simultaneously a solution of
if and only if it is a line with slope 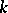 .
.
A rough qualitative representation of the behaviour of the integral curves (cf. Integral curve) of
can be obtained if the isoclines of the given equation are constructed for a sufficiently frequent choice of the parameter  , and if the corresponding inclinations of the integral curves are drawn (the method of isoclines). It is also useful to construct the
, and if the corresponding inclinations of the integral curves are drawn (the method of isoclines). It is also useful to construct the 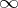 -isocline, defined by the equation
-isocline, defined by the equation 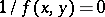 ; at the points of the
; at the points of the 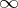 -isocline the integral curves of equation
-isocline the integral curves of equation
have vertical tangents. The (local) extreme points of the solutions of
can lie on the  -isocline only, and the points of inflection of the solution can lie only on the curve
-isocline only, and the points of inflection of the solution can lie only on the curve
 |
For a first-order equation not solvable with respect to the derivative,
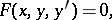 |
the 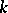 -isocline is defined as the set
-isocline is defined as the set
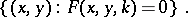 |
In the case of a second-order autonomous system,
 |
the set of points in the phase plane at which the vectors of the phase velocity are collinear is an isocline of the equation
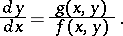 |
References
| [1] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | H.T. Davis, "Introduction to nonlinear differential and integral equations" , Dover, reprint (1962) pp. Chapt. II, §2 |
Isocline. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isocline&oldid=47436