Irregularity indices
for linear systems of ordinary differential equations
Non-negative functions 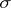 on the space of mappings
on the space of mappings  (or
(or 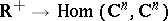 ), integrable on every finite interval, such that
), integrable on every finite interval, such that 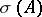 equals zero if and only if the system
equals zero if and only if the system
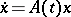 | (*) |
is a regular linear system.
The best known (and easiest to define) such regularity indices are as follows.
1) The Lyapunov irregularity index [1]:
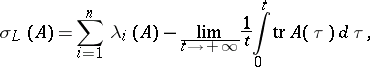 |
where 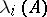 are the Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent) of the system (*), arranged in descending order, while
are the Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent) of the system (*), arranged in descending order, while 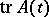 is the trace of the mapping
is the trace of the mapping 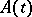 .
.
2) The Perron irregularity index [2]:
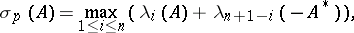 |
where 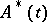 is the adjoint of the mapping
is the adjoint of the mapping 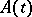 . If the system (*) is a system of variational equations of a Hamiltonian system
. If the system (*) is a system of variational equations of a Hamiltonian system
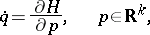 |
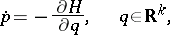 |
then 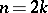 and
and
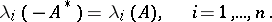 |
Consequently, for a system of variational equations of a Hamiltonian system,
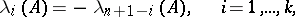 |
is a necessary and sufficient condition for regularity (a theorem of Persidskii).
For other irregularity indices, see [4]–.
References
| [1] | A.M. Lyapunov, "Collected works" , 2 , Moscow-Leningrad (1956) (In Russian) |
| [2] | O. Perron, "Die Ordnungszahlen linearer Differentialgleichungssysteme" Math. Z. , 31 (1929–1930) pp. 748–766 |
| [3] | I.G. Malkin, "Theorie der Stabilität einer Bewegung" , R. Oldenbourg , München (1959) pp. Sect. 79 (Translated from Russian) |
| [4] | B.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [5] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
| [6a] | R.A. Prokhorova, "Estimate of the jump of the highest exponent of a linear system due to exponential perturbations" Differential Eq. , 12 : 3 (1977) pp. 333–338 Differentsial'nye Uravneniya , 12 : 3 (1976) pp. 475–483 |
| [6b] | R.A. Prokhorova, "Stability with respect to a first approximation" Differential Eq. , 12 : 4 (1977) pp. 539–542 Differentsial'nye Uravneniya , 12 : 4 (1976) pp. 766–796 |
Comments
In the case of  , read
, read 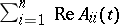 instead of
instead of 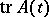 in the definition of
in the definition of 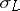 .
.
Irregularity indices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregularity_indices&oldid=47435