Involution algebra
algebra with involution
An algebra 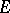 over the field of complex numbers endowed with an involution
over the field of complex numbers endowed with an involution 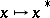 ,
, 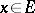 . Some examples are: the algebra of continuous functions on a compact set, in which the involution sends any function to its complex conjugate; the algebra of bounded linear operators on a Hilbert space, in which the involution sends any operator to its adjoint; the group algebra of a locally compact group; and the algebra of measures on a locally compact group. The element
. Some examples are: the algebra of continuous functions on a compact set, in which the involution sends any function to its complex conjugate; the algebra of bounded linear operators on a Hilbert space, in which the involution sends any operator to its adjoint; the group algebra of a locally compact group; and the algebra of measures on a locally compact group. The element 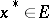 is called the conjugate, or adjoint, of
is called the conjugate, or adjoint, of  . An element
. An element 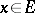 is called self-adjoint, or Hermitian, if
is called self-adjoint, or Hermitian, if 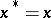 , and normal if
, and normal if 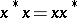 . If
. If 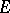 contains a unit element 1, then an element
contains a unit element 1, then an element 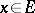 such that
such that 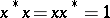 is called unitary. The set
is called unitary. The set 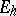 of Hermitian elements of
of Hermitian elements of 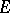 is a real vector subspace of
is a real vector subspace of 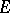 , and any
, and any 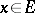 can be uniquely written in the form
can be uniquely written in the form 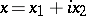 , where
, where 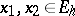 . In this case
. In this case 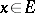 is normal if and only if
is normal if and only if 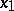 and
and 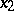 commute. Every element of the form
commute. Every element of the form 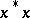 is Hermitian, and so is the unit element. If
is Hermitian, and so is the unit element. If  is invertible, then so is
is invertible, then so is 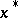 , and
, and 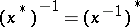 . The spectrum of any Hermitian element (cf. Spectrum of an element) is symmetric about the real axis. An involution algebra
. The spectrum of any Hermitian element (cf. Spectrum of an element) is symmetric about the real axis. An involution algebra 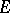 is called a total involution algebra if the spectrum of any element of the form
is called a total involution algebra if the spectrum of any element of the form 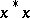 ,
, 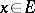 , is contained in the set of non-negative real numbers. Examples of total involution algebras are: the involution algebra of continuous functions on a compact set; the involution algebra of bounded linear operators on a Hilbert space; and group algebras of compact and commutative locally compact groups. The group algebras of non-compact semi-simple Lie groups are not total involution algebras. A commutative involution algebra
, is contained in the set of non-negative real numbers. Examples of total involution algebras are: the involution algebra of continuous functions on a compact set; the involution algebra of bounded linear operators on a Hilbert space; and group algebras of compact and commutative locally compact groups. The group algebras of non-compact semi-simple Lie groups are not total involution algebras. A commutative involution algebra 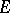 is a total involution algebra if and only if all its maximal ideals are symmetric, or if and only if all characters of
is a total involution algebra if and only if all its maximal ideals are symmetric, or if and only if all characters of 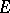 are Hermitian. Every
are Hermitian. Every 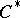 -algebra is a total involution algebra.
-algebra is a total involution algebra.
A subset 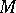 of an involution algebra
of an involution algebra 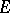 is called an involution set if
is called an involution set if 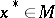 for all
for all 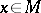 . A mapping
. A mapping 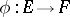 of involution algebras is called an involution mapping if
of involution algebras is called an involution mapping if 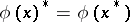 for all
for all 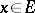 . The kernel of an involution homomorphism of involution algebras is a symmetric two-sided ideal. Every symmetric one-sided ideal is two-sided and the quotient algebra of an involution algebra by a symmetric ideal admits the structure of an involution algebra in a natural way. The radical (cf. Radical of rings and algebras) of an involution algebra is a symmetric ideal. An involution subalgebra
. The kernel of an involution homomorphism of involution algebras is a symmetric two-sided ideal. Every symmetric one-sided ideal is two-sided and the quotient algebra of an involution algebra by a symmetric ideal admits the structure of an involution algebra in a natural way. The radical (cf. Radical of rings and algebras) of an involution algebra is a symmetric ideal. An involution subalgebra 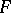 of an involution algebra
of an involution algebra 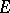 is an involution algebra. Let
is an involution algebra. Let 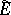 be the direct sum of an involution algebra
be the direct sum of an involution algebra 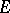 and the field
and the field 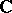 , in which the linear operations and the involution are defined componentwise and the multiplication is given by
, in which the linear operations and the involution are defined componentwise and the multiplication is given by
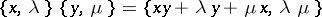 |
for all 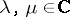 ,
, 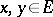 . Then
. Then 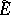 is an involution algebra with a unit element.
is an involution algebra with a unit element.
A linear functional 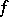 on an involution algebra is called Hermitian if
on an involution algebra is called Hermitian if 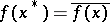 for all
for all 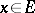 , and positive if
, and positive if 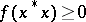 for all
for all 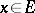 . The set
. The set 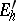 of Hermitian linear functionals on
of Hermitian linear functionals on 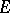 is a real vector subspace of
is a real vector subspace of 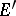 , the dual of
, the dual of 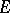 , and
, and 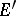 is the direct sum of the subspaces
is the direct sum of the subspaces 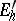 and
and 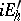 . If
. If 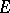 has a unit 1, then every positive functional
has a unit 1, then every positive functional 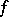 on
on 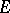 is Hermitian and
is Hermitian and 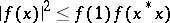 for all
for all 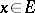 . If
. If 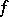 is a positive functional on an involution algebra
is a positive functional on an involution algebra 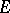 , then
, then 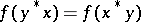 and
and 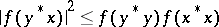 for all
for all 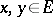 .
.
Let 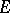 be an involution algebra equipped with a norm making
be an involution algebra equipped with a norm making 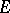 into a normed algebra and satisfying the condition
into a normed algebra and satisfying the condition 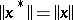 for all
for all 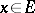 . Then
. Then 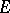 is called a normed algebra with involution. If
is called a normed algebra with involution. If 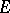 is complete with respect to this norm, then
is complete with respect to this norm, then 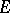 is called a Banach algebra with involution. Every normed algebra with involution
is called a Banach algebra with involution. Every normed algebra with involution 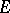 can be imbedded in a Banach algebra with involution
can be imbedded in a Banach algebra with involution 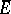 containing
containing 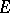 as a dense involution subalgebra.
as a dense involution subalgebra. 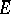 is uniquely defined up to an isometric involution isomorphism.
is uniquely defined up to an isometric involution isomorphism. 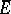 is called the completion of
is called the completion of 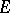 . If
. If 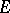 is a Banach algebra with involution having an approximate identity, then every positive linear functional
is a Banach algebra with involution having an approximate identity, then every positive linear functional 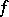 on
on 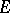 is continuous and can be extended to a positive linear functional on
is continuous and can be extended to a positive linear functional on 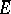 . If
. If 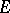 has a unit 1 and
has a unit 1 and  , then for any positive linear functional
, then for any positive linear functional 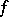 on
on  ,
, 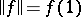 and
and 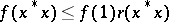 , where
, where 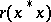 is the spectral radius of
is the spectral radius of 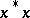 (see Banach algebra).
(see Banach algebra).
A Hermitian element of a total involution algebra has a real spectrum. For any maximal closed left ideal 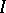 in a total involution algebra
in a total involution algebra 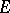 with a unit there is a positive linear functional on
with a unit there is a positive linear functional on 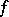 on
on 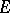 such that
such that 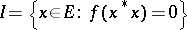 . An element
. An element  in a total involution algebra
in a total involution algebra 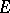 is left-invertible in
is left-invertible in 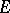 if and only if
if and only if 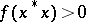 for all non-zero positive functionals
for all non-zero positive functionals 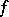 on
on 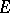 . The radical of a total involution algebra
. The radical of a total involution algebra 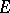 coincides with the set of elements
coincides with the set of elements  such that
such that 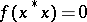 for all positive linear functionals
for all positive linear functionals 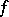 on
on 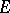 . A Banach algebra with involution
. A Banach algebra with involution 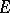 with a unit 1 is a total involution algebra if and only if
with a unit 1 is a total involution algebra if and only if 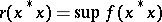 , where the supremum is taken over the set of positive linear functionals
, where the supremum is taken over the set of positive linear functionals 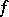 on
on 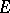 for which
for which 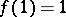 .
.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Dixmier, "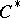 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [3] | V. Pták, "Banach algebras with involution" Manuscripta Math. , 6 : 3 (1972) pp. 245–290 |
| [4] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 2 , Springer (1979) |
Comments
A (Banach, normed) algebra with involution is also called an involutive (Banach, normed) algebra. If in an involutive Banach algebra 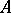 one has
one has 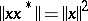 for all
for all 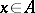 , then
, then 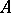 is called a
is called a 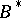 -algebra.
-algebra.
Let 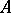 be a Banach algebra. A left-approximate identity in
be a Banach algebra. A left-approximate identity in 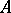 is a net
is a net 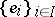 of elements of
of elements of 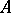 (cf. Net (directed set)) such that
(cf. Net (directed set)) such that 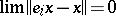 for all
for all 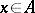 . A right-approximate identity is similarly defined, using
. A right-approximate identity is similarly defined, using 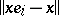 . A left- and right-approximate identity is simply called an approximate identity. Every
. A left- and right-approximate identity is simply called an approximate identity. Every  -algebra has an approximate identity.
-algebra has an approximate identity.
An algebra with involution 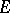 is also termed a symmetric algebra, and a total involution algebra is also called a completely symmetric algebra. Correspondingly, a homomorphism of algebras with involution
is also termed a symmetric algebra, and a total involution algebra is also called a completely symmetric algebra. Correspondingly, a homomorphism of algebras with involution 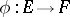 is called a symmetric homomorphism if
is called a symmetric homomorphism if 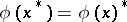 for all
for all 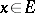 . Unfortunately, the term symmetric algebra is also sometimes used to mean a total involution algebra.
. Unfortunately, the term symmetric algebra is also sometimes used to mean a total involution algebra.
A symmetric ideal of 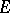 is an ideal
is an ideal 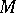 such that
such that 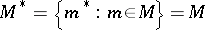 .
.
References
| [a1] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
Involution algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Involution_algebra&oldid=47429