Inversion of a series

To obtain, for a given power series

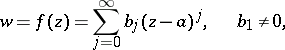(1)

a series for the inverse function 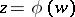in the form

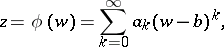(2)

where , ,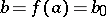

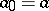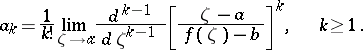The series (2) is called the inverse of the series (1), or the Lagrange series. The more general problem of finding the expansion of an arbitrary composite analytic function 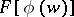is solved by the Bürmann–Lagrange series. If the disc of convergence of (1) is 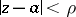, then the series (2) converges in the disc 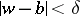, where 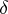is the distance of the point 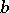from the image of the circle 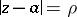under the mapping .

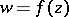If the function 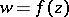is expanded as a series of the form

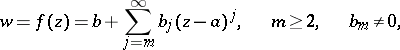(3)

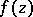that is, if is a critical point for , then the inverse function 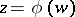has an algebraic branch point of order at 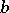, and inversion of (3) is only possible in the form of a Puiseux series:

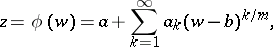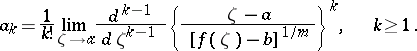The problem of inversion of a Laurent series in negative and positive integer powers of 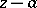is solved similarly in the case when the series has only finitely many negative (or positive) powers (see [1]).

For analytic functions of several complex variables 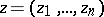, , 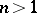problems of inversion can be put in various ways. For example, if 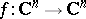is a non-singular (that is, the rank of the Jacobi matrix 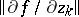is equal to ) holomorphic mapping of a neighbourhood of zero in 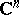into 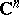, , then in some neighbourhood of zero there exists an inverse holomorphic function , which can be described in the form of a multi-dimensional Bürmann–Lagrange series (see [3]).

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian)
[2]	A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) pp. Chapt. 3, Abschnitt 2
[3]	E.E. Soltan, "The expansion of holomorphic functions in multi-dimensional Bürmann–Lagrange series" , Holomorphic functions of several complex variables , Krasnoyarsk (1972) pp. 129–137; 212 (In Russian)