Inverse parabolic partial differential equation

An equation of the form

(*)

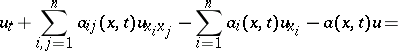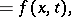where the form is positive definite. The variable plays the role of "inverse" time. The substitution reduces equation (*) to the usual parabolic form. Parabolic equations of "mixed" type occur, for example, is a direct parabolic equation for and an inverse parabolic equation for , with degeneracy of the order for .

Comments

The Cauchy problem for an equation (*) is a well-known example of an ill-posed problem (cf. Ill-posed problems). For a discussion of the backward heat equation (cf. also Thermal-conductance equation)

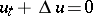( being the Laplace operator) see [a1].

References

[a1]	L.E. Payne, "Improperly posed problems in partial differential equations" , SIAM (1975)