Interior-point methods in mathematical programming

A class of theoretically and practically efficient techniques for solving certain structured convex programming problems, including linear programming problems. Besides, ideas arising from research on interior-point methods have influenced the areas of non-convex programming, combinatorial optimization and decomposition methods. A recent survey is given in [a6].

Interior-point methods originate from K.R. Frisch (1955), [a1]. To solve a convex programming problem

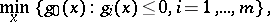where are convex functions, he introduced the logarithmic barrier function

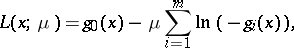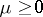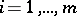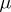parametrized by . Under certain conditions, concerning the existence of a Slater point (i.e. a point that satisfies the Slater regularity condition , ; cf. also Mathematical programming) and boundedness of level-sets, this function has a minimizer for fixed ; for 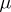converging to zero, it has been shown that converges to an optimal solution. The set

is called the central path of the optimization problem. The generic interior-point method, or path-following method, works as follows. Given a value 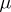, compute an approximate minimizer of 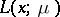; reduce 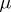and proceed. Different methods are obtained by: using different barrier functions, varying the updating scheme for , the method used for minimizing the barrier function (mainly a variant of the Newton method), and the criterion that judges approximation to the exact minimizer. The latter aspect is related to the use of neighbourhoods of the central path.

Interior-point techniques were extensively investigated in the 1960{}s (see [a2]) and early 1970{}s. Computational difficulties with minimizing efficiently caused these methods to get out of sight. In 1984, N.K. Karmarkar [a3] proved a variant of an interior-point method to have polynomial worst-case complexity when applied to the linear programming problem. Thereafter, many new variants have been theoretically analyzed as well as implemented. Especially, primal-dual interior-point algorithms (i.e., methods generating primal and dual solutions in each iteration) proved to be extremely efficient to solve large-scale linear programming problems, see [a4].

The analysis that shows which properties make it possible to prove polynomial convergence of interior-point methods for classes of convex programming problems should mainly be attributed to Yu. Nesterov and A.S. Nemirovskii, [a5]. These classes include: convex quadratic programming with linear and/or quadratic constraints, geometric programming, entropy optimization, -optimization, and semi-definite optimization. The self-concordance condition they introduced for convex (barrier) functions essentially shows when such a function can be efficiently (i.e., with quadratic convergence) minimized using the Newton method.

References

[a1]	K.R. Frisch, "The logarithmic potential method for convex programming" Institute of Economics, Univ. Oslo (1955)
[a2]	A.V. Fiacco, G.P. McCormick, "Nonlinear programming: sequential unconstrained minimization techniques" , Classics in Applied Math. , 4 , SIAM (1990) (reprint)
[a3]	N.K. Karmarkar, "A new polynomial-time algorithm for linear programming" Combinatorica , 4 (1984) pp. 373–395
[a4]	I.J. Lustig, R.E. Marsten, D.F. Shanno, "Interior point methods: computational state of the art" ORSA J. Computing , 6 (1994) pp. 1–15
[a5]	Yu. Nesterov, A.S. Nemirovskii, "Interior point polynomial algorithms in convex programming" , Studies in Applied Mathematics , 13 , SIAM (1994) (In Russian)
[a6]	"Interior point view of mathematical programming" T. Terlaky (ed.) , Kluwer Acad. Publ. (1996)
[a7]	D. den Hertog, "Interior point approach to linear, quadratic and convex programming" , Kluwer Acad. Publ. (1994)