Integral representations of linear operators
Let 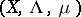 and
and 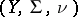 be
be 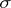 -finite measure spaces (cf. Measure space) and let
-finite measure spaces (cf. Measure space) and let 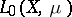 and
and 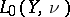 be the spaces of the complex-valued
be the spaces of the complex-valued 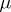 -measurable functions on
-measurable functions on  and the complex-valued
and the complex-valued  -measurable functions on
-measurable functions on 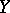 , respectively. A linear subspace
, respectively. A linear subspace 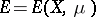 of
of 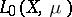 is called an ideal space, or a solid linear subspace, of
is called an ideal space, or a solid linear subspace, of 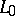 if
if 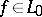 ,
, 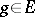 and
and 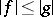 ,
, 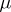 -a.e., imply
-a.e., imply 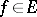 . The classical
. The classical 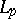 -spaces (
-spaces (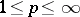 ), the Orlicz spaces and, more generally, Banach function spaces (cf. also Orlicz space; Banach space) are typical examples of normed ideal spaces.
), the Orlicz spaces and, more generally, Banach function spaces (cf. also Orlicz space; Banach space) are typical examples of normed ideal spaces.
If 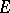 ,
, 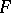 are ideal spaces contained in
are ideal spaces contained in 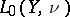 and
and 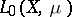 , respectively, then
, respectively, then 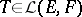 , the linear space of all linear operators from
, the linear space of all linear operators from 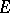 into
into 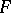 , is called an integral operator, kernel operator, if there exists a
, is called an integral operator, kernel operator, if there exists a 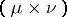 -measurable function
-measurable function 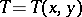 ,
, 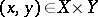 , such that for all
, such that for all 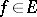 and
and 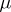 -a.e. with respect to
-a.e. with respect to  ,
, 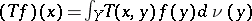 .
.
Integral operators, also known as integral transforms, play an important role in analysis. It is a natural question to ask: Which 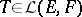 are integral operators? J. von Neumann [a5] was the first to show that for the ideal spaces
are integral operators? J. von Neumann [a5] was the first to show that for the ideal spaces 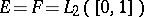 the identity operator does not admit an integral representation. He proved, however, that a bounded self-adjoint linear operator
the identity operator does not admit an integral representation. He proved, however, that a bounded self-adjoint linear operator 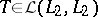 is unitarily equivalent (cf. also Unitarily-equivalent operators) to an integral operator if and only if
is unitarily equivalent (cf. also Unitarily-equivalent operators) to an integral operator if and only if  is an element of the limit spectrum of
is an element of the limit spectrum of 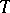 .
.
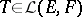 is called a positive linear operator if for all
is called a positive linear operator if for all 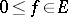 one has
one has 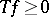 (
(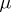 -a.e.). An integral operator
-a.e.). An integral operator 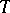 with kernel
with kernel  (
(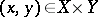 ) is positive if and only if
) is positive if and only if 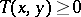 ,
, 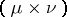 -a.e.;
-a.e.;  is called regular if
is called regular if 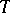 maps order-bounded sets into order-bounded sets, i.e., for all
maps order-bounded sets into order-bounded sets, i.e., for all  there exists a
there exists a 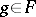 such that for all
such that for all 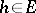 satisfying
satisfying 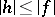 , one has
, one has 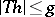 ;
; 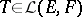 is ordered bounded if and only if
is ordered bounded if and only if 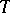 can be written as the difference of two positive linear operators if and only if its modulus
can be written as the difference of two positive linear operators if and only if its modulus 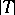 , where for all
, where for all 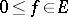 ,
, 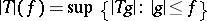 , is a positive linear operator mapping
, is a positive linear operator mapping 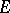 into
into 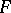 .
.
The following theorem holds: An integral operator 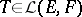 is regular if and only if its modulus
is regular if and only if its modulus 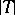 is a positive linear operator mapping
is a positive linear operator mapping 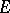 into
into 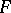 . In that case, the kernel of
. In that case, the kernel of 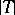 is given by the modulus
is given by the modulus 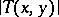 (
(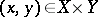 ) of the kernel of
) of the kernel of 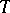 .
.
An integral transform need not be regular, as is shown, for instance, by the Fourier transform and the Hilbert transform.
Integral operators can be characterized via a continuity property: 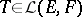 is a linear integral operator if and only if
is a linear integral operator if and only if 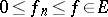 (
(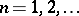 ) and
) and 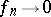 in
in  -measure as
-measure as 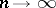 imply
imply 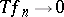 (
(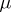 -a.e.) as
-a.e.) as 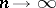 .
.
An earlier version of this theorem for bilinear forms is due to H. Nakano [a4]. For regular linear operators defined on KB-spaces (cf. also 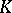 -space), the result appeared in a slightly different form in a paper by G.Ya. Lozonovskii [a3]. The present version is due to A.V. Bukhvalov [a1]. A pure measure-theoretic proof and related results were given by A. Schep [a6]. For details and further results see [a2].
-space), the result appeared in a slightly different form in a paper by G.Ya. Lozonovskii [a3]. The present version is due to A.V. Bukhvalov [a1]. A pure measure-theoretic proof and related results were given by A. Schep [a6]. For details and further results see [a2].
References
| [a1] | A.V. Bukhvalov, "A criterion for integral representability of linear operators" Funktsional. Anal. i Prilozhen. , 9 : 1 (1975) pp. 51 (In Russian) |
| [a2] | "Vector lattices and integral operators" S.S. Kutateladze (ed.) , Mathematics and its Applications , 358 , Kluwer Acad. Publ. (1996) |
| [a3] | G.Ya. Lozanovsky, "On almost integral operators in 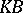 -spaces" Vestnik Leningrad Gos. Univ. , 7 (1966) pp. 35–44 (In Russian) -spaces" Vestnik Leningrad Gos. Univ. , 7 (1966) pp. 35–44 (In Russian) |
| [a4] | H. Nakano, "Product spaces of semi-ordered linear spaces" J. Fac. Sci. Hokkaidô Univ. Ser. I , 12 : 3 (1953) pp. 163–210 |
| [a5] | J. von Neumann, "Charakterisierung des Spektrums eines Integraloperators" , Actualités Sc. et Industr. , 229 , Hermann (1935) |
| [a6] | A.R. Schep, "Kernel operators" Proc. Kon. Nederl. Akad. Wetensch. , A 82 (1979) pp. 39–53 |
Integral representations of linear operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_representations_of_linear_operators&oldid=47381