Integral logarithm
The special function defined, for positive real  ,
,  , by
, by
 |
for  the integrand has at
the integrand has at  an infinite discontinuity and the integral logarithm is taken to be the principal value
an infinite discontinuity and the integral logarithm is taken to be the principal value
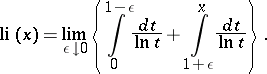 |
The graph of the integral logarithm is given in the article Integral exponential function. For  small:
small:
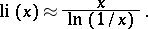 |
The integral logarithm has for positive real  the series representation
the series representation
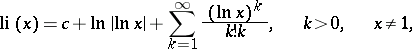 |
where 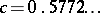 is the Euler constant. As a function of the complex variable
is the Euler constant. As a function of the complex variable  ,
,
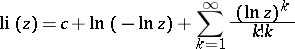 |
is a single-valued analytic function in the complex  -plane with slits along the real axis from
-plane with slits along the real axis from 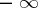 to 0 and from 1 to
to 0 and from 1 to  (the imaginary part of the logarithms is taken within the limits
(the imaginary part of the logarithms is taken within the limits 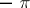 and
and 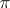 ). The behaviour of
). The behaviour of 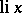 along
along 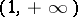 is described by
is described by
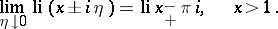 |
The integral logarithm is related to the integral exponential function 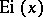 by
by
 |
For real  one sometimes uses the notation
one sometimes uses the notation
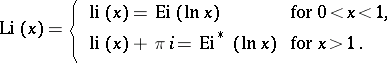 |
For references, see Integral cosine.
Comments
The function 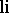 is better known as the logarithmic integral. It can, of course, be defined by the integral (as above) for
is better known as the logarithmic integral. It can, of course, be defined by the integral (as above) for 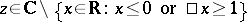 .
.
The series representation for positive  ,
, 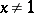 , is then also said to define the modified logarithmic integral, and is the boundary value of
, is then also said to define the modified logarithmic integral, and is the boundary value of 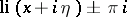 ,
, 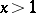 ,
, 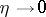 . For real
. For real 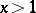 the value
the value  is a good approximation of
is a good approximation of  , the number of primes smaller than
, the number of primes smaller than  (see de la Vallée-Poussin theorem; Distribution of prime numbers; Prime number).
(see de la Vallée-Poussin theorem; Distribution of prime numbers; Prime number).
Integral logarithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_logarithm&oldid=47376