Integral funnel
of a point  for a differential equation
for a differential equation 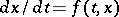
The set of all points lying on the integral curves (cf. Integral curve) passing through 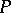 . (By an equation one can mean a system of equations in vector notation with
. (By an equation one can mean a system of equations in vector notation with 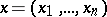 .) If only one integral curve passes through
.) If only one integral curve passes through 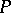 , then the integral funnel consists of this single curve. In the case
, then the integral funnel consists of this single curve. In the case 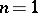 , that is, when
, that is, when  is scalar, the integral funnel consists of points
is scalar, the integral funnel consists of points 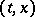 for which
for which 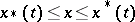 , where
, where 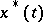 and
and 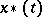 are the upper and lower solutions, that is, the largest and smallest solutions passing through
are the upper and lower solutions, that is, the largest and smallest solutions passing through  .
.
If the function  is continuous (or satisfies the conditions of the Carathéodory existence theorem), then the integral funnel is a closed set. Furthermore, if all the solutions passing through
is continuous (or satisfies the conditions of the Carathéodory existence theorem), then the integral funnel is a closed set. Furthermore, if all the solutions passing through 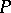 exist on the interval
exist on the interval 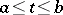 , then this segment of the funnel (the part of the integral funnel defined by the inequalities
, then this segment of the funnel (the part of the integral funnel defined by the inequalities 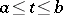 ) and the section of the integral funnel by any plane
) and the section of the integral funnel by any plane 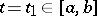 are connected compact sets. Any point on the boundary of the integral funnel can be joined to
are connected compact sets. Any point on the boundary of the integral funnel can be joined to 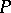 by a piece of the integral curve lying on the boundary of the integral funnel. If the sequence of points
by a piece of the integral curve lying on the boundary of the integral funnel. If the sequence of points 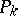 ,
, 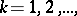 converges to
converges to 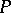 , then the segments of the funnels of the points
, then the segments of the funnels of the points 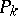 converge to the segment of the funnel of
converge to the segment of the funnel of 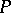 in the sense that for any
in the sense that for any 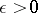 they are contained in an
they are contained in an  -neighbourhood of the segment of the funnel of
-neighbourhood of the segment of the funnel of 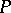 if
if 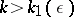 . Analogous properties are possessed by integral funnels for differential inclusions (cf. Differential inclusion)
. Analogous properties are possessed by integral funnels for differential inclusions (cf. Differential inclusion)
 |
under specified hypotheses concerning the set 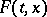 .
.
References
| [1] | E. Kamke, "Zur Theorie der Systeme gewöhnlicher Differentialgleichungen. II" Acta Math. , 58 (1932) pp. 57–85 |
| [2] | M.F. Bokstein, Uchen. Zap. Moskov. Gos. Univ. Ser. Mat. , 15 (1939) pp. 3–72 |
| [3] | C.C. Pugh, "Funnel sections" J. Differential Eq. , 19 : 2 (1975) pp. 270–295 |
Comments
References
| [a1] | A.F. Filippov, "Differential equations with discontinuous righthand sides" , Kluwer (1988) pp. 16 (Translated from Russian) |
Integral funnel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_funnel&oldid=47373