Integral curve

The graph of a solution of a normal system

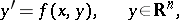of ordinary differential equations. For example, the integral curves of the equation

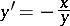are the circles 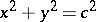, where is an arbitrary constant. The integral curve is often identified with the solution. The geometric meaning of the integral curves of a scalar equation

(*)

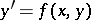is the following. The equation (*) defines a direction field on the plane, that is, a field of direction vectors such that at each point the tangent of the angle of inclination of the vector with the -axis is equal to . The integral curves of (*) are then the curves that at each point have a tangent coinciding with the vector of the direction field at this point. The integral curves of (*) fill out the entire region in which the function 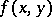satisfies conditions ensuring the existence and uniqueness of the Cauchy problem; the curves nowhere intersect one another and are nowhere tangent to one another.

References

[1]	I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian)

Comments

A normal system of differential equations is a system of differential equations of the form

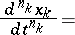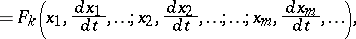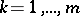, such that the function 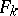only depends on the 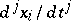for , .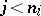

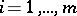References

[a1]	G. Birkhoff, G.-C. Rota, "Ordinary differential equations" , Ginn (1962) pp. Chapt. V §5
[a2]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) pp. §§3.6, 3.51, 4.7, A.5