Initial conditions
Conditions imposed in formulating the Cauchy problem for differential equations. For an ordinary differential equation in the form
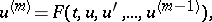 | (1) |
the initial conditions prescribe the values of the derivatives (Cauchy data):
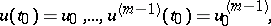 | (2) |
where 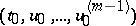 is an arbitrary fixed point of the domain of definition of the function
is an arbitrary fixed point of the domain of definition of the function 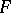 ; this point is known as the initial point of the required solution. The Cauchy problem (1), (2) is often called an initial value problem.
; this point is known as the initial point of the required solution. The Cauchy problem (1), (2) is often called an initial value problem.
For a partial differential equation, written in normal form with respect to a distinguished variable 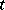 ,
,
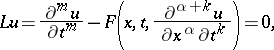 |
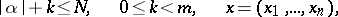 |
the initial conditions consist in prescribing the values of the derivatives (Cauchy data)
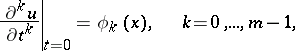 |
of the required solution 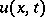 on the hyperplane
on the hyperplane 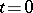 (the support of the initial conditions).
(the support of the initial conditions).
Comments
References
| [a1] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
| [a2] | S. Mizohata, "The theory of partial differential equations" , Cambridge Univ. Press (1973) (Translated from Japanese) |
Initial conditions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Initial_conditions&oldid=47359