Information, exactness of reproducibility of
A measure of the quality of information transmission from an information source (cf. Information, source of) to a receiver (addressee) over a communication channel. The criteria relevant to the exactness of reproducibility of information in the theory of information transmission are usually treated statistically, by isolating the class 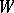 of admissible joint distributions for pairs
of admissible joint distributions for pairs 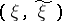 in the set of all probability measures on the product
in the set of all probability measures on the product 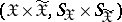 , where
, where 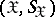 is the measurable space of values of a communication
is the measurable space of values of a communication 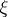 generated by the source, and
generated by the source, and  is the measurable space of values of the communication
is the measurable space of values of the communication 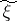 received. Exactness of reproducibility of information is often defined in terms of a distortion measure
received. Exactness of reproducibility of information is often defined in terms of a distortion measure 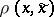 ,
, 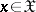 ,
, 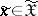 , which is a non-negative measurable function of
, which is a non-negative measurable function of  and
and 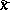 . The set of admissible communications
. The set of admissible communications 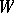 is then specified by the formula
is then specified by the formula
 | (1) |
for a given 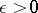 .
.
In particular, when 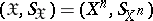 and
and 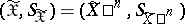 , one often uses a componentwise condition for the exactness of reproducibility of information, namely
, one often uses a componentwise condition for the exactness of reproducibility of information, namely
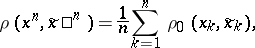 |
where 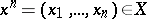 ,
, 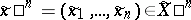 ,
, 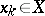 ,
, 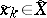 ,
, 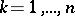 , and where
, and where 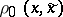 ,
, 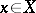 ,
, 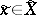 , is again a non-negative measurable function. In this case, instead of condition (1) one sometimes uses the following condition:
, is again a non-negative measurable function. In this case, instead of condition (1) one sometimes uses the following condition:
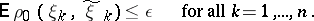 | (2) |
In the case when 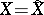 and
and
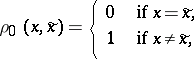 |
the conditions (1) and (2) turn into restrictions on the mean or maximal probability of erroneous decoding (cf. Erroneous decoding, probability of) of separate components of the communication, respectively. In the case of sources with continuous spaces (such as a Gaussian source), it is often assumed that 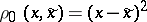 .
.
References
| [1] | R. Gallagher, "Information theory and reliable communication" , Wiley (1968) |
| [2] | T. Berger, "Rate distortion theory" , Prentice-Hall (1971) |
Comments
References
| [a1] | I. Csiszar, J. Körner, "Information theory. Coding theorems for discrete memoryless systems" , Akad. Kiado (1981) |
Information, exactness of reproducibility of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information,_exactness_of_reproducibility_of&oldid=47350