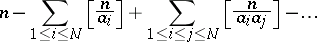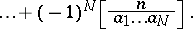A method for calculating the number 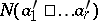 of objects which do not have any of the given properties
of objects which do not have any of the given properties  , according to the following formula:
, according to the following formula:
 | (1) |
where 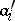 denotes the absence of property
denotes the absence of property 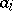 ,
, 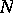 is the total number of objects,
is the total number of objects, 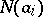 is the number of objects having property
is the number of objects having property 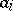 ,
, 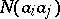 is the number of objects having both properties
is the number of objects having both properties 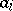 and
and 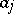 , etc. (see [3]). The inclusion-and-exclusion principle yields a formula for calculating the number of objects having exactly
, etc. (see [3]). The inclusion-and-exclusion principle yields a formula for calculating the number of objects having exactly 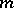 properties out of
properties out of  ,
, 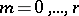 :
:
 | (2) |
where 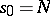 ,
, 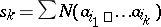 , and the summation is performed over all
, and the summation is performed over all 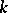 -tuples
-tuples 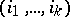 such that
such that 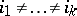 ,
, 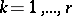 , i.e.
, i.e.
The method for calculating 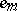 according to (2) is also referred to as the inclusion-and-exclusion principle. This principle is used in solving combinatorial and number-theoretic problems [1]. For instance, given a natural number
according to (2) is also referred to as the inclusion-and-exclusion principle. This principle is used in solving combinatorial and number-theoretic problems [1]. For instance, given a natural number  and natural numbers
and natural numbers 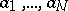 such that
such that 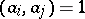 if
if 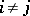 , the number of natural numbers
, the number of natural numbers 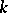 ,
, 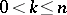 , that are not divisible by
, that are not divisible by 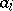 ,
, 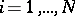 , is, according to (1):
, is, according to (1):
The inclusion-and-exclusion principle also serves to solve problems of inversion [2], [3].
References
| [1] | M. Hall jr., "Combinatorial theory" , Wiley (1986) |
| [2] | H.J. Ryser, "Combinatorial mathematics" , Wiley & Math. Assoc. Amer. (1963) |
| [3] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
How to Cite This Entry:
Inclusion-and-exclusion principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inclusion-and-exclusion_principle&oldid=47325
This article was adapted from an original article by S.A. Rukova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article of objects which do not have any of the given properties
of objects which do not have any of the given properties  , according to the following formula:
, according to the following formula:

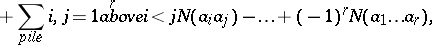
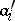 denotes the absence of property
denotes the absence of property 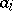 ,
, 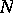 is the total number of objects,
is the total number of objects, 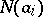 is the number of objects having property
is the number of objects having property 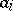 ,
, 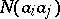 is the number of objects having both properties
is the number of objects having both properties 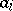 and
and 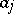 , etc. (see [3]). The inclusion-and-exclusion principle yields a formula for calculating the number of objects having exactly
, etc. (see [3]). The inclusion-and-exclusion principle yields a formula for calculating the number of objects having exactly 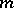 properties out of
properties out of  ,
, 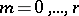 :
:

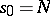 ,
, 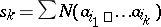 , and the summation is performed over all
, and the summation is performed over all 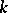 -tuples
-tuples 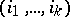 such that
such that 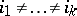 ,
, 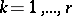 , i.e.
, i.e.
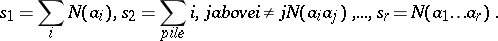
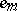 according to (2) is also referred to as the inclusion-and-exclusion principle. This principle is used in solving combinatorial and number-theoretic problems [1]. For instance, given a natural number
according to (2) is also referred to as the inclusion-and-exclusion principle. This principle is used in solving combinatorial and number-theoretic problems [1]. For instance, given a natural number  and natural numbers
and natural numbers 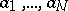 such that
such that 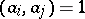 if
if 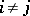 , the number of natural numbers
, the number of natural numbers 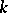 ,
, 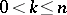 , that are not divisible by
, that are not divisible by 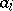 ,
, 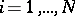 , is, according to (1):
, is, according to (1):