Implicative propositional calculus

A propositional calculus using only the primitive connective 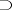(implication). Examples of an implicative propositional calculus are the complete (or classical) implicative propositional calculus given by the axioms

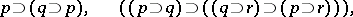and the rules of inference: modus ponens and substitution; another example is the positive implicative propositional calculus given by the axioms

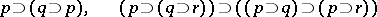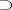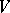and the same rules of inference. Every implicative formula, that is, a formula only containing the connective , is deducible in complete (or positive) implicative propositional calculus if and only if it is deducible in classical (respectively, intuitionistic) propositional calculus. For any finite set of variables, among the formulas with variables in there is only a finite number of pairwise inequivalent ones in the positive implicative propositional calculus (see [3]). There exist undecidable finitely-axiomatizable implicative propositional calculi (see [4]).

References

[1]	A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956)
[2]	J. Łukasiewicz, A. Tarski, "Untersuchungen über den Aussagenkalkül" C.R. Soc. Sci. Letters Varsovie, Cl. III , 23 (1930) pp. 30–50
[3]	A. Diego, "Sur les algèbres de Hilbert" , Gauthier-Villars (1966) ((translated from the Spanish))
[4]	M.D. Gladstone, "Some ways of constructing a propositional calculus of any required degree of unsolvability" Trans. Amer. Math. Soc. , 118 (1965) pp. 192–210