Imbedded word

occurrence

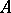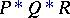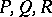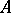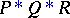A word of a special type containing complete information about the position of one word inside another. More precisely, an occurrence in an alphabet is a word of the form , where are words in , while is not a letter of that alphabet. The occurrence is also an occurrence of the word 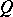into the word 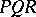. The word 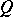is called the base of this occurrence; the words 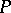and 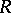are known as the left and right wings, respectively. The concept of an occurrence may be made the base of a system of concepts which is convenient for the study of the syntactic structure of words of one type or another.

References

[1]	A.A. Markov, "Theory of algorithms" , Israel Program Sci. Transl. (1961) (Translated from Russian) (Also: Trudy Mat. Inst. Steklov. 42 (1954))
[2]	N.M. Nagornyi, "The theory of algorithms" , Kluwer (1988) (Translated from Russian)

Comments

The phrase "imbedded word" is not in common use in English. The (English) translation [1] speaks of an entry of one word in another and of left and right delimiters (rather than occurrence, left and right wings, which are used in the (English) translation [2]). Other English-speaking authors tend to refer to an occurrence of one word as a subword (or segment) of another.

References

[a1]	S. Eilenberg, "Automata, languages and machines" , A , Acad. Press (1974)
[a2]	J.L. Britton, "The word problem" Ann. of Math. , 77 (1963) pp. 16–32