Identical truth

logical truth, tautology

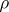A property of formulas in the language of predicate calculus, meaning that the formulas are true in all interpretations and for all admissible values of their free variables. For example, for a formula containing only one -place predicate symbol and variables of one sort (that is, variables which are interpreted in the same domain of variation), any pair , where is an arbitrary non-empty set and is an arbitrary binary relation on , is an interpretation. Arbitrary elements of are admissible values for the free variables. Truth of a formula 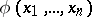at values (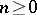) of the variables , respectively, is defined by induction on the structure of the formula, as follows. (Here the free variables run through the set and the predicate symbol denotes the relation .)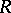

Suppose that a formula 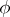is given, as well as a finite sequence 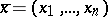of variables containing all the free variables of 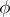; let denote the set of all finite sequences 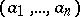of elements of at which 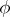is true in . A set of the form can be constructed inductively as follows (here it is assumed that the logical symbols in 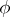are , , ):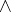

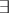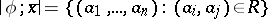if 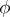has the form ;

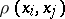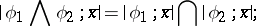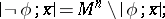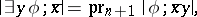where , , 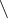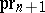denote, respectively, intersection, difference and projection along the 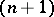-st coordinate (that is, the image with respect to the mapping 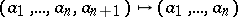) of sets.

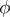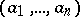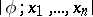Identical truth for a formula with free variables then means that for any interpretation , every sequence of elements of belongs to the set . For 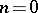the set is either empty or a singleton. For example, the formula

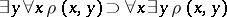is an identical truth. The converse implication is not an identically-true formula.

In the case where an interpretation is fixed, a formula is sometimes called identically true if it is true in the given interpretation for any values of its free variables.

References

[1]	S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)
[2]	J.R. Shoenfield, "Mathematical logic" , Addison-Wesley (1967)