Hutchinson equation

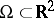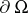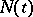Suppose a population inhabits a bounded homogeneous area with piecewise-smooth boundary . Assume that its food base regularly restores itself to a certain level, whilst the migration factor is so high that complete mixing takes place. In [a1] it was postulated that under these idealized conditions the variation in population density , where is the current size of the population and 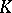is the average number of the population, which depends upon the size of the habitat and the amount of food available, obeys the law

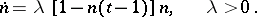Here, 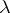is the Malthusian coefficient of linear growth, provided that the age of sexual maturity of females is taken as the unit of time. This equation is called the Hutchinson equation. For 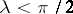, the attractor of positive solutions of the equation is its unit state of equilibrium, whilst for 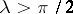it is an orbitally exponentially stable cycle. This assertion is mainly based on the results of numerical analysis (significantly less was obtained by purely mathematical methods, [a2]).

As 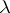increases, the Hutchinson cycle acquires a distinctive relaxation character, which is evident from the following facts [a3]. Assume, for the sake of being specific, that 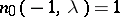and 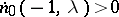. Then the largest value 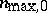of the function is reached at :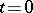

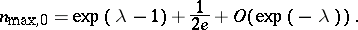The smallest value, 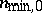of the function 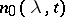is realized at 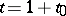, where

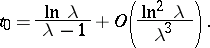The asymptotic equality

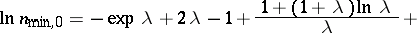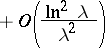is valid.

If migration across the habitat's boundary is forbidden, the migration factor results in the boundary value problem

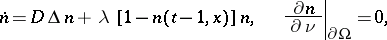where 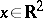, 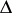is the Laplace operator, 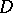is the mobility coefficient, and is the direction of the external normal. When 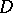decreases, Hutchinson's cycle loses stability as a result of spacial perturbations connected with the appearance of so-called self-organization regimes, which are simultaneously complexly and regularly arranged towards spacial and temporal variables [a3].

References

[a1]	G. Hutchinson, "Circular causal systems in ecology" Ann. N.Y. Acad. Sci. , 50 (1948–1950) pp. 221–246
[a2]	J. Hale, "Theory of functional differential equations" , Springer (1977) (Edition: Second)
[a3]	A.Yu. Kolesov, Yu.S. Kolesov, "Relaxation oscillation in mathematical models of ecology" Proc. Steklov Inst. Math. , 199 : 1 (1995) (In Russian)