Hopf fibration

A locally trivial fibration for . This is one of the earliest examples of locally trivial fibrations, introduced by H. Hopf in [1]. These mappings induce trivial mappings in homology and cohomology; however, they are not homotopic to the null mapping, which follows from the fact that their Hopf invariant is non-trivial. The creation of the mappings requires the so-called Hopf construction.

Let be the join of two spaces and , which has natural coordinates , where , , . Here, for example, , where is the suspension of . The Hopf construction associates with a mapping the mapping given by .

Suppose that mappings are defined for by means of multiplications: in the complex numbers for 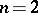, in the quaternions for , and in the Cayley numbers for . Then 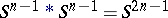, and the Hopf mapping is defined as

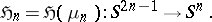The Hopf mapping , , 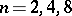is a locally trivial fibration with fibre 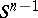. If 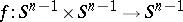is a mapping of bidegree 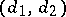, then the Hopf invariant of the mapping 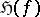is 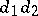. In particular, the Hopf invariant of the Hopf fibration is 1.

Sometimes the Hopf fibration is defined as the mapping given by the formula , . This mapping is a locally trivial fibration with fibre . For 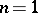one obtains the classical Hopf fibration .

References

[1]	H. Hopf, "Ueber die Abbildungen von Sphären niedriger Dimension" Fund. Math. , 25 (1935) pp. 427–440
[2]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)