Homology sequence
An exact sequence, infinite on both sides, of homology groups of three complexes, connected by a short exact sequence. Let 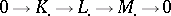 be an exact sequence of chain complexes in an Abelian category. Then there are morphisms
be an exact sequence of chain complexes in an Abelian category. Then there are morphisms
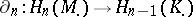 |
defined for all  . They are called connecting (or boundary) morphisms. Their definition in the category of modules is especially simple: For
. They are called connecting (or boundary) morphisms. Their definition in the category of modules is especially simple: For 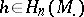 a pre-image
a pre-image  is chosen;
is chosen; 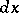 will then be the image of an element
will then be the image of an element 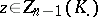 whose homology class is
whose homology class is 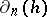 . The sequence of homology groups
. The sequence of homology groups
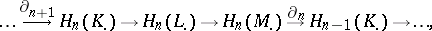 |
constructed with the aid of the connecting morphisms, is exact; it is called the homology sequence. Thus, the homology groups form a homology functor on the category of complexes.
Cohomology sequences are defined in a dual manner.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
Homology sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_sequence&oldid=47262