Holomorphic form
of degree  on a complex manifold
on a complex manifold 
A differential form  of type
of type  that satisfies the condition
that satisfies the condition  , i.e. a form that can be written in the local coordinates
, i.e. a form that can be written in the local coordinates  on
on  as
as
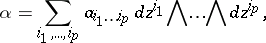 |
where 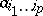 are holomorphic functions (cf. Holomorphic function). The holomorphic forms of degree
are holomorphic functions (cf. Holomorphic function). The holomorphic forms of degree  form a vector space
form a vector space  over the field
over the field 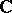 ;
;  is the space of holomorphic functions on
is the space of holomorphic functions on  .
.
On a compact Kähler manifold  the space
the space 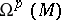 coincides with the space
coincides with the space  of harmonic forms of type
of harmonic forms of type 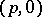 (cf. Harmonic form), hence
(cf. Harmonic form), hence 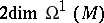 is the first Betti number of
is the first Betti number of  [1]. Holomorphic forms on a Riemann surface
[1]. Holomorphic forms on a Riemann surface  are also known as differentials of the first kind; if
are also known as differentials of the first kind; if 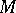 is compact,
is compact,  is equal to its genus (cf. Genus of a curve).
is equal to its genus (cf. Genus of a curve).
The spaces 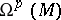 ,
, 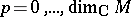 , form a locally exact complex with respect to the operator
, form a locally exact complex with respect to the operator 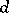 , known as the holomorphic de Rham complex. If
, known as the holomorphic de Rham complex. If 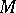 is a Stein manifold, then the cohomology spaces of this complex are isomorphic to the complex cohomology spaces
is a Stein manifold, then the cohomology spaces of this complex are isomorphic to the complex cohomology spaces 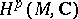 , and
, and  if
if  [2].
[2].
Holomorphic forms with values in some analytic vector bundle (cf. Vector bundle, analytic) 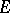 over
over 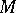 are defined in the same manner (here, holomorphic
are defined in the same manner (here, holomorphic  -forms are holomorphic sections of the bundle). The germs of holomorphic forms of degree
-forms are holomorphic sections of the bundle). The germs of holomorphic forms of degree 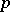 with values in
with values in  form a locally free analytic sheaf
form a locally free analytic sheaf  . The Dolbeault complex of forms of type
. The Dolbeault complex of forms of type 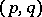 ,
,  , with values in
, with values in  is a fine resolution of this sheaf, so that
is a fine resolution of this sheaf, so that
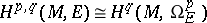 |
(the Dolbeault–Serre theorem [1], [4]).
The definition of holomorphic forms can be extended to complex-analytic spaces. It is sufficient to do this for local models, i.e. for the case of a space 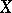 that is an analytic subspace of a domain
that is an analytic subspace of a domain  . The sheaf of germs of holomorphic
. The sheaf of germs of holomorphic  -forms
-forms 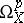 in
in  is defined as
is defined as
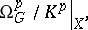 |
where 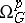 is the sheaf of germs of holomorphic
is the sheaf of germs of holomorphic  -forms in
-forms in 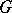 , while
, while 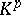 consists of the germs of forms of the type
consists of the germs of forms of the type
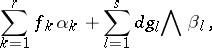 |
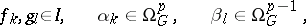 |
where 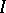 is the sheaf of ideals which define
is the sheaf of ideals which define 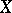 . The holomorphic de Rham complex of
. The holomorphic de Rham complex of  is also defined, but it is not locally exact. For this complex to be locally exact at a point
is also defined, but it is not locally exact. For this complex to be locally exact at a point  starting from the
starting from the 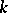 -th degree it is sufficient that
-th degree it is sufficient that 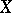 has, in a neighbourhood of
has, in a neighbourhood of  , a holomorphic contraction onto a local analytic set
, a holomorphic contraction onto a local analytic set  for which
for which  [3].
[3].
References
| [1] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
| [2] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [3] | H.J. Reiffen, "Das Lemma von Poincaré für holomorphe Differentialformen auf komplexen Räumen" Math. Z. , 101 (1967) pp. 269–284 |
| [4] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Holomorphic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorphic_form&oldid=47244